题目内容
6.喜欢钻研的小亮对75°角的三角函数发生了兴趣,他想:75度虽然不是特殊角,但和特殊角有着密切的关系,能否通过特殊角的三角函数值求75°的正弦值呢?经研究,他发现:sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°,于是他大胆猜想:sin(α+β)=sinαcosβ+cosαsinβ(α和β为锐角).将图1(a)等积变形为图1(b)可用于勾股定理的证明,现将这两幅图分别“压扁”成图2(a)和图2(b).如图,锐角为α的直角三角形斜边为m,锐角为β的直角三角形斜边为n,请你借助图2(a)和图2(b)证明上述结论能成立.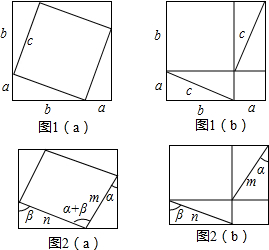
分析 根据平行四边形的面积公式求出图2(a)中?ABCD的面积,根据矩形的面积公式求出图2(b)中矩形ABCD与CEFG的面积,由图2(a)与图2(b)中空白部分的面积相等即可证明sin(α+β)=sinαcosβ+cosαsinβ.
解答 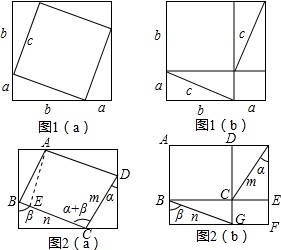 解:如图2(a),原来内部的正方形变成了一个平行四边形,m,n为相邻两边,其夹角为α+β,
解:如图2(a),原来内部的正方形变成了一个平行四边形,m,n为相邻两边,其夹角为α+β,
作?ABCD的高AE,则AE=AB•sinB=msin(180°-α-β)=msin(α+β),
则S?ABCD=BC•AE=n•msin(α+β)=mnsin(α+β).
如图2(b),原来的两个小正方形变成了两个矩形ABCD与CEFG,
则S矩形ABCD=BC•AB=nsinβ•mcosα=mncosαsinβ,
S矩形CEFG=CE•CG=msinα•ncosβ=mnsinαcosβ,
∵图2(a)与图2(b)中空白部分的面积相等,
∴mnsin(α+β)=mncosαsinβ+mnsinαcosβ,
化简得sin(α+β)=sinαcosβ+cosαsinβ.
点评 本题考查了解直角三角形,图形面积的计算,理解两幅图分别“压扁”成图2(a)和图2(b)后的形状得出它们空白部分的面积相等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.关于x,y的二元一次方程组$\left\{\begin{array}{l}{x+y=4k}\\{x-y=8k}\end{array}\right.$的解也是二元一次方程2x+3y=6的解,则k的值是( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
15.下列函数是二次函数的是( )
| A. | y=8x2+1 | B. | y=2x-3 | C. | y=3x2+$\frac{1}{{x}^{2}}$ |
16.n个连续偶数按规律排成表:
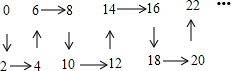
根据规律,从2016到2018,箭头的方向依次应为( )
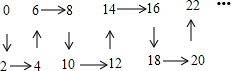
根据规律,从2016到2018,箭头的方向依次应为( )
| A. | ↑→ | B. | →↑ | C. | ↓→ | D. | →↓ |
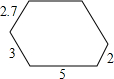 如图,一个六边形的每个内角都是120°,连续四边的长依次是2.7、3、5、2,则该六边形的周长是20.7.
如图,一个六边形的每个内角都是120°,连续四边的长依次是2.7、3、5、2,则该六边形的周长是20.7.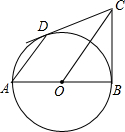 如图,已知AB为⊙O的直径,CB、CD分别切⊙O于点B、D.求证:AD∥OC.
如图,已知AB为⊙O的直径,CB、CD分别切⊙O于点B、D.求证:AD∥OC.