题目内容
3.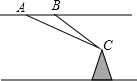 如图,飞机的飞行高度为2500米,在A点处测得某电视塔尖点C的俯角为30°,保持方向不变前进1200米到达B点时测得该电视塔尖点C的俯角为45°.请计算电视塔的高度(结果保留整数,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,飞机的飞行高度为2500米,在A点处测得某电视塔尖点C的俯角为30°,保持方向不变前进1200米到达B点时测得该电视塔尖点C的俯角为45°.请计算电视塔的高度(结果保留整数,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 易得BC=CF,那么利用30°的正切值即可求得CF长.
解答 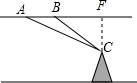 解:过C作CF⊥AB交AB的延长线于F,
解:过C作CF⊥AB交AB的延长线于F,
∵∠BCF=90°,∠FBC=45°,
∴BC=CF,
∵∠CAF=30°,
∴tan 30°=$\frac{CF}{AB+BF}$=$\frac{CF}{1200+CF}$=$\frac{\sqrt{3}}{3}$,
解得CF=600$\sqrt{3}$+600(m).
∴电视塔的高度=2500-(600$\sqrt{3}$+600)≈861m,
答:电视塔的高度约为861米.
点评 此题考查了考查俯角的定义,要求学生能借助俯角构造直角三角形并解直角三角形.注意方程思想与数形结合思想的应用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
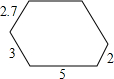 如图,一个六边形的每个内角都是120°,连续四边的长依次是2.7、3、5、2,则该六边形的周长是20.7.
如图,一个六边形的每个内角都是120°,连续四边的长依次是2.7、3、5、2,则该六边形的周长是20.7. 如图是一个铁制零件的三视图及尺寸标注.
如图是一个铁制零件的三视图及尺寸标注.