一个口袋中有 3 个黑球和若干个白球.在不允许将球倒出来数的前提下.小明为估计其中的白球数.采用了如下的方法:从口袋中随机摸出一球.记下颜色.然后把它放回口袋中.摇匀后再随机摸出一球.记下颜色.-.不断重复上述过程．小明共摸了100次.其中25次摸到黑球．根据上述数据.小明可估计口袋中的白球大约有( )A．12 个B．15 个C．9 个题目和参考答案——青夏教育精英家教网—

题目内容

12．一个口袋中有 3 个黑球和若干个白球，在不允许将球倒出来数的前提下，小明为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色，…，不断重复上述过程．小明共摸了100次，其中25次摸到黑球．根据上述数据，小明可估计口袋中的白球大约有（　　）

A．

12 个

B．

15 个

C．

9 个

D．

10 个

分析小明共摸了100次，其中25次摸到黑球，则有75次摸到白球；摸到黑球与摸到白球的次数之比为1：3，由此可估计口袋中黑球和白球个数之比为1：3；即可计算出白球数．

解答解：∵小明共摸了100次，其中25次摸到黑球，则有75次摸到白球，
∴摸到黑球与摸到白球的次数之比为1：3，
∵这个口袋中有3个黑球，
∴共有白球3×3=9个，
故选C．

点评本题考查的是通过样本去估计总体，只需将样本“成比例地放大”为总体即可．

练习册系列答案

a²×a⁵=a¹⁰

$\sqrt{a+b}=\sqrt{a}+\sqrt{b}$

C．

（-a³）⁴=a¹²

D．

$\sqrt{a^2}=a$

19．如图①，AB⊥BD，CD⊥BD，垂足分别为B、D，AD、BC相交于点E，过点E作EF⊥BD．
（1）猜想$\frac{1}{AB}$、$\frac{1}{CD}$、$\frac{1}{EF}$这三个量之间的数量关系并证明．
（2）若将图①中的垂直改为斜交，如图②，AB∥CD，AD、BC相交于点E，过点E作EF∥AB交BD于点F，试问（1）中的数量关系还成立吗？说明理由．
（3）试找出S_△ABD，S_△BED，S_△BDC之间的关系式，并说明理由．

7．如图1，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB边上的中点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．
（1）四边形BECD是什么特殊四边形？说明你的理由；
（2）当∠A=45°时，四边形BECD是正方形；
（3）如图2，过点C作CH⊥AB于H，过点B作BK⊥MN于K，动点P、Q分别从C、B两点同时出发，点P自C→D→H→C停止，点Q自B→K→E→B停止，已知CD=10，CH=8，在运动过程中，点P、Q的运动路程分别为a、b（ab≠0），若C、B、P、Q四点为顶点的四边形是平行四边形，则a与b满足的数量关系式是b=24-a．

17．

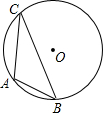如图，已知⊙O的直径为8cm，A、B、C三点在⊙O上，且∠ACB=30°，则AB长为（　　）

4．

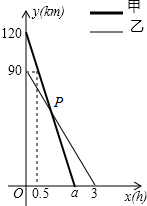在一条笔直的公路旁依次有A、B、C三个村庄，甲、乙两人同时分别从A、B两村出发，甲骑摩托车，乙骑电动车沿公路匀速驶向C村，最终到达C村．甲、乙两人到C村的距离y₁，y₂（km）与行驶时间x（h）之间的函数关系如图所示，以下分析错误的是（　　）

	A．	A、C两村间的距离为120km
	B．	点P的坐标为（1，60）
	C．	点P的意义表示经过1小时甲与乙相遇且距C村60km
	D．	乙在行驶过程中，仅有一次机会距甲10km

1．

如图，若将左边的正方形剪成两个直角三角形和两个四边形后，恰好能拼成右边的矩形．设a=2，则正方形的边长为$\sqrt{5}$+3．

2．

如图，用若干个全等的正五边形可以拼成一个环状，图中所示的是前3个正五边形的拼接情况，要完全拼成一个圆环还需要的正五边形个数是（　　）

试题分类