题目内容
1. 如图,若将左边的正方形剪成两个直角三角形和两个四边形后,恰好能拼成右边的矩形.设a=2,则正方形的边长为$\sqrt{5}$+3.
如图,若将左边的正方形剪成两个直角三角形和两个四边形后,恰好能拼成右边的矩形.设a=2,则正方形的边长为$\sqrt{5}$+3.
分析 从图中可以看出,正方形的边长=a+b,所以面积=(a+b)2,矩形的长和宽分别是2b+a,b,面积=b(a+2b),两图形面积相等,列出方程得,(a+b)2=b(a+2b),其中a=2,求b的值,即可求得正方形的面积.
解答 解:根据图形和题意可得:
(a+b)2=b(a+2b),
其中a=2,
则方程是(2+b)2=b(2+2b)
解得:b=1±$\sqrt{5}$(负数舍去),
所以正方形的边长为:a+b=2+1+$\sqrt{5}$=3+$\sqrt{5}$.
故答案为:$\sqrt{5}$+3.
点评 此题主要考查了图形的剪拼,本题的关键是从两图形中,找到两图形的边长的值,然后利用面积相等列出等式求方程,解得b的值,从而求出边长,求面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.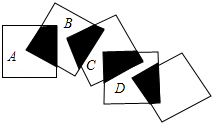 将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是( )cm2.
将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是( )cm2.
 将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是( )cm2.
将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是( )cm2.| A. | 2cm2 | B. | 4cm2 | C. | 6cm2 | D. | 8cm2 |
12.一个口袋中有 3 个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,…,不断重复上述过程.小明共摸了100次,其中25次摸到黑球.根据上述数据,小明可估计口袋中的白球大约有( )
| A. | 12 个 | B. | 15 个 | C. | 9 个 | D. | 10 个 |
16.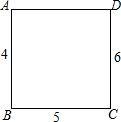 如图所示,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数为4,BC上的数为5,CD上的数为6,则AD上的数应为( )
如图所示,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数为4,BC上的数为5,CD上的数为6,则AD上的数应为( )
 如图所示,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数为4,BC上的数为5,CD上的数为6,则AD上的数应为( )
如图所示,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数为4,BC上的数为5,CD上的数为6,则AD上的数应为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
13. 如图,沿AC方向修山路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A、C、E在一条直线上,那么开挖点E与D的距离是( )
如图,沿AC方向修山路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A、C、E在一条直线上,那么开挖点E与D的距离是( )
 如图,沿AC方向修山路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A、C、E在一条直线上,那么开挖点E与D的距离是( )
如图,沿AC方向修山路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A、C、E在一条直线上,那么开挖点E与D的距离是( )| A. | 500sin55°米 | B. | 500cos35°米 | C. | 500cos55°米 | D. | 500tan55°米 |
10.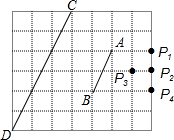 如图6×7的方格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )
如图6×7的方格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )
 如图6×7的方格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )
如图6×7的方格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )| A. | P1 | B. | P2 | C. | P3 | D. | P4 |
11.下列运算正确的是( )
| A. | 2x+3y=5xy | B. | x2•x3=x6 | C. | x5÷x=x4 | D. | (x-y)2=x2-y2 |
 如图,将弧长为6π的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计),则圆锥形纸帽的底面半径是3.
如图,将弧长为6π的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计),则圆锥形纸帽的底面半径是3.