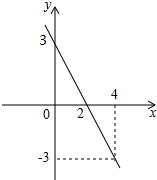
题目内容
12．二次函数y=ax2+bx+c的图象与x轴交于点A（1，0），与y轴交于点C（0，-5），且经过点D（2，7）．（1）求此二次函数的解析式；
（2）请你写出一种平移方法，使平移后的抛物线经过原点，并写出平移后抛物线的解析式．
分析 （1）把已知三点坐标代入抛物线求出a，b，c的值，即可确定出解析式；
（2）根据平移规律确定出抛物线解析式即可．
解答 解：（1）把A，C及D坐标代入抛物线解析式得：$\left\{\begin{array}{l}{a+b+c=0}\\{c=-5}\\{4a+2b+c=7}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=1}\\{b=4}\\{c=-5}\end{array}\right.$，
则二次函数解析式为y=x2+4x-5；
（2）抛物线向下平移5个单位经过原点，得到解析式为y=x2+4x．
点评 此题考查了抛物线与x轴的交点，以及二次函数图象与几何变换，熟练掌握运算法则是解本题的关键．
练习册系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
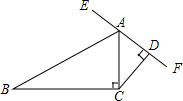如图，已知AC⊥BC，CD⊥AD，∠B=30°，∠ACD=40°，求图中四边形ABCD的外角的度数．
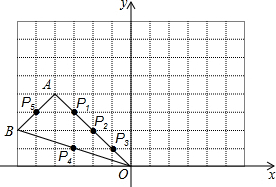如图，在边长为1的小正方形组成的网格中，△AOB的顶点都在格点上，点A、B的坐标分别为（-4，4）、（-6，2）．请按要求完成下列各题：
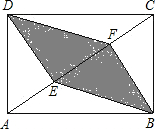如图，一块矩形场地ABCD，现测得边长AB与AD之比为$\sqrt{2}$：1，DE⊥AC于点E，BF⊥AC于点F，连接BE，DF．现计划在四边形DEBF区域内种植花草．