题目内容
14.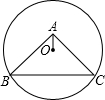 如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{13}$ | C. | 4 | D. | 3$\sqrt{2}$ |
分析 连接AO并延长,交BC于D,连接OB,根据垂径定理得到BD=$\frac{1}{2}$BC=3,根据等腰直角三角形的性质得到AD=BD=3,根据勾股定理计算即可.
解答 解: 连接AO并延长,交BC于D,连接OB,
连接AO并延长,交BC于D,连接OB,
∵AB=AC,
∴AD⊥BC,
∴BD=$\frac{1}{2}$BC=3,
∵△ABC是等腰直角三角形,
∴AD=BD=3,
∴OD=2,
∴OB=$\sqrt{B{D}^{2}+O{D}^{2}}$=$\sqrt{13}$,
故选:B.
点评 本题考查的是垂径定理、等腰直角三角形的性质,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
2.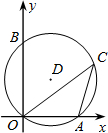 如图,点O为坐标原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为$\widehat{OBA}$上的一点(不与O、A两点重合),连接OC,AC,则cosC的值为( )
如图,点O为坐标原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为$\widehat{OBA}$上的一点(不与O、A两点重合),连接OC,AC,则cosC的值为( )
 如图,点O为坐标原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为$\widehat{OBA}$上的一点(不与O、A两点重合),连接OC,AC,则cosC的值为( )
如图,点O为坐标原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为$\widehat{OBA}$上的一点(不与O、A两点重合),连接OC,AC,则cosC的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
3.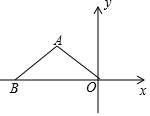 如图,已知等腰△ABO的底边BO在x轴上,且BO=8,AB=AO=5,点A的坐标是( )
如图,已知等腰△ABO的底边BO在x轴上,且BO=8,AB=AO=5,点A的坐标是( )
 如图,已知等腰△ABO的底边BO在x轴上,且BO=8,AB=AO=5,点A的坐标是( )
如图,已知等腰△ABO的底边BO在x轴上,且BO=8,AB=AO=5,点A的坐标是( )| A. | (-3,4) | B. | (3,-4) | C. | (-4,3) | D. | (4,-3) |
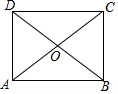 如图,在矩形ABCD中,对角线AC、BD相交于点O,且OA=OD.若∠OAD=50°,求∠OAB的度数.
如图,在矩形ABCD中,对角线AC、BD相交于点O,且OA=OD.若∠OAD=50°,求∠OAB的度数.