题目内容
2.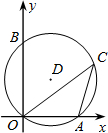 如图,点O为坐标原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为$\widehat{OBA}$上的一点(不与O、A两点重合),连接OC,AC,则cosC的值为( )
如图,点O为坐标原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A,B,O三点,点C为$\widehat{OBA}$上的一点(不与O、A两点重合),连接OC,AC,则cosC的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
分析 直接利用圆周角定理结合勾股定理得出AB的长,进而求出答案.
解答  解:连接AB,
解:连接AB,
∵点A的坐标为(3,0),点B的坐标为(0,4),
∴AO=3,BO=4,
∴AB=5,
∵∠C=∠OBA,
∴cosC的值为:cos∠OBA=$\frac{BO}{AB}$=$\frac{4}{5}$.
故选:D.
点评 此题主要考查了圆周角定理以及解直角三角形,正确作出辅助线是解题关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
14.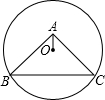 如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
 如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{13}$ | C. | 4 | D. | 3$\sqrt{2}$ |
11. 据新华网消息,2016年6月20日,使用中国自主芯片制造的超级计算机“神威太湖之光”以浮点运算速度每秒930000000亿次登上全球500强榜首,数字930000000用科学记数法可表示为( )
据新华网消息,2016年6月20日,使用中国自主芯片制造的超级计算机“神威太湖之光”以浮点运算速度每秒930000000亿次登上全球500强榜首,数字930000000用科学记数法可表示为( )
 据新华网消息,2016年6月20日,使用中国自主芯片制造的超级计算机“神威太湖之光”以浮点运算速度每秒930000000亿次登上全球500强榜首,数字930000000用科学记数法可表示为( )
据新华网消息,2016年6月20日,使用中国自主芯片制造的超级计算机“神威太湖之光”以浮点运算速度每秒930000000亿次登上全球500强榜首,数字930000000用科学记数法可表示为( )| A. | 9.3×108 | B. | 93×107 | C. | 0.93×109 | D. | 9.3×109 |
12. 有这样一道选择题:熊猫一只前掌趾的根数是( )?A.3根 B.4根 C.5根 D.6根
有这样一道选择题:熊猫一只前掌趾的根数是( )?A.3根 B.4根 C.5根 D.6根
四个选项中只有一个正确,在你不知道熊猫前掌趾根数或者知道熊猫前掌趾根数的情况下,任选一个选择支,你答对的概率分别是( )
 有这样一道选择题:熊猫一只前掌趾的根数是( )?A.3根 B.4根 C.5根 D.6根
有这样一道选择题:熊猫一只前掌趾的根数是( )?A.3根 B.4根 C.5根 D.6根四个选项中只有一个正确,在你不知道熊猫前掌趾根数或者知道熊猫前掌趾根数的情况下,任选一个选择支,你答对的概率分别是( )
| A. | $\frac{1}{4}$,1 | B. | $\frac{1}{4}$,$\frac{1}{4}$ | C. | 1,$\frac{1}{4}$ | D. | $\frac{1}{4}$,$\frac{1}{2}$ |
 如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=20°,则∠1=50°.
如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=20°,则∠1=50°.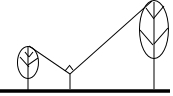 如图,身高1.5米的人站在两棵树之间,距较高的树5米,距较矮的树3米,若此人观察的树梢所成的视线的夹角是90°,且较矮的树高4米,那么较高的树有多少米?
如图,身高1.5米的人站在两棵树之间,距较高的树5米,距较矮的树3米,若此人观察的树梢所成的视线的夹角是90°,且较矮的树高4米,那么较高的树有多少米?