题目内容
16. 如图,AB,CD相交于点O,AC∥DB,E,F为AB上的两点,且AE=BF,OC=OD,求证:CE=DF.
如图,AB,CD相交于点O,AC∥DB,E,F为AB上的两点,且AE=BF,OC=OD,求证:CE=DF.
分析 可先证明△AOC≌△BOD,得到AC=BD,再证明△AEC≌△BFD,可证明CE=DF.
解答 证明:
∵AC∥BD,
∴∠A=∠B,
在△AOC和△BOD中
$\left\{\begin{array}{l}{∠A=∠B}\\{∠AOC=∠BOD}\\{OC=OD}\end{array}\right.$
∴△AOC≌△BOD(AAS),
∴AC=BD,
在△AEC和△BFD中
$\left\{\begin{array}{l}{AE=BF}\\{∠A=∠B}\\{AC=BD}\end{array}\right.$
∴△AEC≌△BFD(SAS),
∴CE=DF.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
7.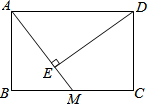 如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )
如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )
 如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )
如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )| A. | 2 | B. | $\frac{12}{5}$ | C. | $\sqrt{13}$ | D. | $\sqrt{5}$ |
4.为了让山更绿、水更清,确保到2015年实现全省森林覆盖率达到63%的目标,已知2013年全省森林覆盖率为60.05%,设从2013年起全省森林覆盖率的年平均增长率为x,则可列方程( )
| A. | 60.05(1+2x)=63% | B. | 60.05(1+3x)=63 | C. | 60.05(1+x)2=63% | D. | 60.05%(1+x)2=63% |
8.下列说法正确的是( )
| A. | 4的算术平方根是$\sqrt{2}$ | B. | $\sqrt{16}$的平方根是±2 | ||
| C. | 27的立方根是±3 | D. | $\sqrt{9}$的平方根是±3 |
6.在下列运算中,正确的是( )
| A. | (x4)2=x6 | B. | x3•x2=x6 | C. | x2+x2=2x4 | D. | x6÷x2=x4 |
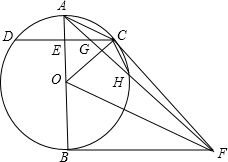 如图,已知AB是⊙O的直径,C是⊙O上任一点(不与A,B重合),AB⊥CD于E,BF为⊙O的切线,OF∥AC,连结AF,FC,AF与CD交于点G,与⊙O交于点H,连结CH.
如图,已知AB是⊙O的直径,C是⊙O上任一点(不与A,B重合),AB⊥CD于E,BF为⊙O的切线,OF∥AC,连结AF,FC,AF与CD交于点G,与⊙O交于点H,连结CH.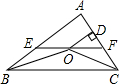 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB与E,交AC于F,过点O作OD⊥AC于D,下列四个结论:其中正确的结论是( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB与E,交AC于F,过点O作OD⊥AC于D,下列四个结论:其中正确的结论是( ) 如图,△ABC中,AB=AC,且AC上的中线BD把这个三角形的周长分成了12cm和6cm的两部分,求这个三角形的腰长和底边的长.
如图,△ABC中,AB=AC,且AC上的中线BD把这个三角形的周长分成了12cm和6cm的两部分,求这个三角形的腰长和底边的长.