题目内容
7.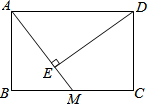 如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )
如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )| A. | 2 | B. | $\frac{12}{5}$ | C. | $\sqrt{13}$ | D. | $\sqrt{5}$ |
分析 首先根据矩形的性质,求得AD∥BC,即可得到∠DAE=∠AMB,又由∠DEA=∠B,根据有两角对应相等的三角形相似,可得△DAE∽△AMB,由△ABM∽△ADE可以得到$\frac{AM}{AD}=\frac{AB}{DE}$,根据勾股定理可以求得AD的长,继而得到答案.
解答 解:在矩形ABCD中,
∵M是边BC的中点,BC=3,AB=2,
∴AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\sqrt{{2}^{2}+(\frac{3}{2})^{2}}$=$\frac{5}{2}$,
∵AD∥BC,
∴∠DAE=∠AMB,
∵∠DEA=∠B=90°,
∴△DAE∽△AMB,
∴$\frac{AM}{AD}=\frac{AB}{DE}$,
即$\frac{\frac{5}{2}}{3}=\frac{2}{DE}$,
∴DE=$\frac{12}{5}$.
故选:B.
点评 此题考查了相似三角形的判定与性质,以及矩形的性质.解题时要注意识图,准确应用数形结合思想.

练习册系列答案
相关题目
17.若$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$是二元一次方程组的解,则这个方程组是( )
| A. | $\left\{\begin{array}{l}{x-3y=5}\\{2x+y=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x-y=5}\\{x+y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y=x-3}\\{y-2x=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2y}\\{x=3y+1}\end{array}\right.$ |
15.若点A(2,-2),B(-1,-2),则直线AB与x轴和y轴的位置关系分别是( )
| A. | 相交,相交 | B. | 平行,平行 | C. | 平行,垂直相交 | D. | 垂直相交,平行 |
 如图,长方形的长AD=9,宽AB=3,则图中阴影部分的面积为9.
如图,长方形的长AD=9,宽AB=3,则图中阴影部分的面积为9.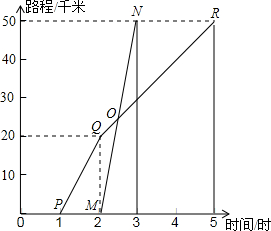 如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.
如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.
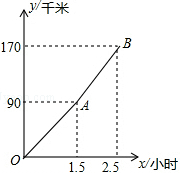 “五一节”期间,张老师一家自驾游去了离家170千米的某地,下面他们一家离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
“五一节”期间,张老师一家自驾游去了离家170千米的某地,下面他们一家离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象. 如图,AB,CD相交于点O,AC∥DB,E,F为AB上的两点,且AE=BF,OC=OD,求证:CE=DF.
如图,AB,CD相交于点O,AC∥DB,E,F为AB上的两点,且AE=BF,OC=OD,求证:CE=DF.