题目内容
11.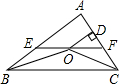 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB与E,交AC于F,过点O作OD⊥AC于D,下列四个结论:其中正确的结论是( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB与E,交AC于F,过点O作OD⊥AC于D,下列四个结论:其中正确的结论是( )①EF=BE+CF;
②∠BOC=90°+$\frac{1}{2}$∠A;
③设OD=m,AE+AF=n,则S△AEF=mn.
④EF不能成为△ABC的中位线.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由在△ABC中,∠ABC和∠ACB的平分线相交于点O,根据角平分线的定义与三角形内角和定理,即可求得②∠BOC=90°+$\frac{1}{2}$∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正确;由角平分线定理与三角形面积的求解方法,即可求得③设OD=m,AE+AF=n,则S△AEF=$\frac{1}{2}$mn,故③错误;E、F不可能是三角形ABC的中点,则EF不能为中位线故④正确.
解答 解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°-$\frac{1}{2}$∠A,
∴∠BOC=180°-(∠OBC+∠OCB)=90°+$\frac{1}{2}$∠A;故②正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,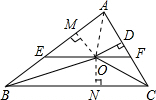
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=$\frac{1}{2}$AE•OM+$\frac{1}{2}$AF•OD=$\frac{1}{2}$OD•(AE+AF)=$\frac{1}{2}$mn;故③错误;
∵E、F不可能是三角形ABC的中点,∴EF不可能是△ABC的中位线.
所以④正确.
综上可知其中正确的结论是①②④,
故选C.
点评 此题考查了三角形中位线定理的运用,以及平行线的性质、等腰三角形的判定与性质.此题难度适中,解题的关键是注意数形结合思想的应用.

 名校课堂系列答案
名校课堂系列答案| A. | 6 | B. | 12 | C. | 16 | D. | 18 |
| A. | (-2ab)3=8a3b3 | B. | (2mn2)2=4m2n4 | C. | (-x2y)4=x8y4 | D. | ($\frac{1}{2}$m3n2)2=$\frac{1}{4}$m6n4 |
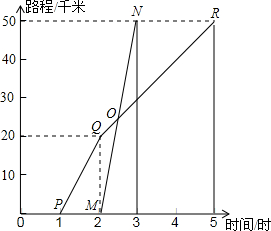 如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.
如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.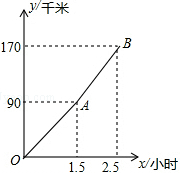 “五一节”期间,张老师一家自驾游去了离家170千米的某地,下面他们一家离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
“五一节”期间,张老师一家自驾游去了离家170千米的某地,下面他们一家离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.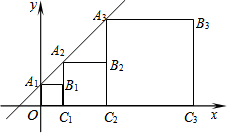 如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,AnBnCnCn-1按所示的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B2015的坐标是(22015-1,22014).
如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,AnBnCnCn-1按所示的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B2015的坐标是(22015-1,22014). 如图,AB,CD相交于点O,AC∥DB,E,F为AB上的两点,且AE=BF,OC=OD,求证:CE=DF.
如图,AB,CD相交于点O,AC∥DB,E,F为AB上的两点,且AE=BF,OC=OD,求证:CE=DF. 如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量.小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°.你能够计算这块地的面积吗?
如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量.小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°.你能够计算这块地的面积吗?