题目内容
如图，在△ABC中，D是AB上一点，AD=AC，AE⊥CD，垂足为E，F是BC中点，探究BD与EF的关系．并说明理由．考点：三角形中位线定理,等腰三角形的性质
专题：
分析：根据三角形的中位线定理，在三角形中准确应用，并且求证E为CD的中点，再求证EF为△BCD的中位线．
解答：解：BD∥EF，且BD=2EF．理由如下：
在△ACD中，∵AD=AC，AE⊥CD，
∴E为CD的中点，
又∵F是CB的中点，
∴EF为△BCD的中位线，
∴EF∥BD，EF=
BD，即BD=2EF．
在△ACD中，∵AD=AC，AE⊥CD，
∴E为CD的中点，
又∵F是CB的中点，
∴EF为△BCD的中位线，
∴EF∥BD，EF=
| 1 |
| 2 |
点评：本题考查了三角形中位线定理和等腰三角形的性质．三角形中位线的性质：三角形的中位线平行于第三边且等于第三边的一半．
练习册系列答案
阅读快车系列答案
相关题目
如图y=-x2+c与x轴相交于A，B两点，顶点C在y轴上，若该抛物线的两个内接正方形ODFE和正方形FHCG如图所示，求c的值．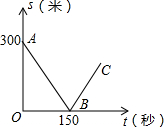
甲、乙两名自行车爱好者准备在一段长为3500米的笔直公路上进行比赛，比赛开始时乙在起点，甲在乙的前面．他们同时出发，匀速前进，已知甲的速度为12米/秒，设甲、乙两人之间的距离为s（米），比赛时间为t（秒），图中的折线表示从两人出发至其中一人先到达终点的过程中s（米）与t（秒）的函数关系．根据图中信息，回答下列问题：
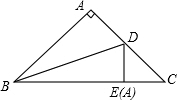如图，等腰直角△ABC中，∠A=90°，AB=AC，把等腰直角△ABC沿BD折叠，使点A落在边BC上的点E处，CE=1，求BC的长．
如图，△ABC的中线AE，BD相交于点G，DF∥BC交AE于点F，求