题目内容
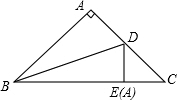 如图,等腰直角△ABC中,∠A=90°,AB=AC,把等腰直角△ABC沿BD折叠,使点A落在边BC上的点E处,CE=1,求BC的长.
如图,等腰直角△ABC中,∠A=90°,AB=AC,把等腰直角△ABC沿BD折叠,使点A落在边BC上的点E处,CE=1,求BC的长.考点:翻折变换(折叠问题),等腰直角三角形
专题:
分析:如图,证明DE=CE=1,AD=DE=1,此为解题的关键性结论;求出DC=
,AB=AC=
+1;再运用勾股定理即可解决问题.
| 2 |
| 2 |
解答: 解:如图,由题意得:
解:如图,由题意得:
AD=DE;∠DEB=∠A=90°;
∵∠A=90°,AB=AC,
∴∠C=45°,∠CDE=90°-45°=45°;
∴DE=CE=1,AD=DE=1;
由勾股定理得:DC2=12+12,
∴DC=
,AB=AC=
+1;
由勾股定理得:BC2=AB2+AC2,
∴BC=
AB=
(
+1)=2+
.
即BC的长为2+
.
 解:如图,由题意得:
解:如图,由题意得:AD=DE;∠DEB=∠A=90°;
∵∠A=90°,AB=AC,
∴∠C=45°,∠CDE=90°-45°=45°;
∴DE=CE=1,AD=DE=1;
由勾股定理得:DC2=12+12,
∴DC=
| 2 |
| 2 |
由勾股定理得:BC2=AB2+AC2,
∴BC=
| 2 |
| 2 |
| 2 |
| 2 |
即BC的长为2+
| 2 |
点评:该题主要考查了翻折变换的性质、勾股定理、等腰直角三角形的性质等几何知识点的应用问题;解题的关键是牢固掌握定理内容,灵活运用定理来分析、解答.

练习册系列答案
相关题目
在
,
,
,-
,3.
,3.1415,2.010101…(相邻两个1之间有1个0)中,无理数有( )
| 25 |
| 2 |
| 11 |
| 3 |
| π |
| 3 |
| •• |
| 25 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列说法正确的是( )
A、“掷一枚硬币正面朝上的概率是
| ||
| B、一组数据2,2,3,6的众数和中位数都是2 | ||
| C、要了解全市人民的低碳生活状况,适宜采用抽样调查的方法 | ||
| D、随机抽取甲、乙两名同学的5次数学成绩,计算得平均分都是90分,方差分别是S2甲=5,S2乙=12,说明乙的成绩较为稳定 |
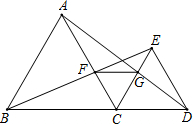 如图,已知点C在线段BD上,在BD的同侧作正△CDE、正△ABC,AC交BE于F,AD交CE于G,连接FG,在这个图形中,不在标注其它字母和添加任何辅助线,由这些条件可推出哪些结论?
如图,已知点C在线段BD上,在BD的同侧作正△CDE、正△ABC,AC交BE于F,AD交CE于G,连接FG,在这个图形中,不在标注其它字母和添加任何辅助线,由这些条件可推出哪些结论? 如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为E,F是BC中点,探究BD与EF的关系.并说明理由.
如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为E,F是BC中点,探究BD与EF的关系.并说明理由.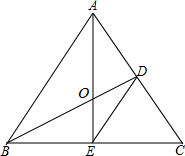 如图,△ABC是等边三角形,BD⊥AC,AE⊥BC,垂足分别为D、E,AE、BD相交于点O,连接DE.
如图,△ABC是等边三角形,BD⊥AC,AE⊥BC,垂足分别为D、E,AE、BD相交于点O,连接DE. 如图,等边△ABC中,D、E分别在AB、BC边上,且AD=2BE=4,连接DE,并将线段DE绕点E顺时针旋转60°,得到线段EF,连接CF,取EF中点G,连接AG,延长CF交AG于点H.若AH=
如图,等边△ABC中,D、E分别在AB、BC边上,且AD=2BE=4,连接DE,并将线段DE绕点E顺时针旋转60°,得到线段EF,连接CF,取EF中点G,连接AG,延长CF交AG于点H.若AH=