题目内容
 如图y=-x2+c与x轴相交于A,B两点,顶点C在y轴上,若该抛物线的两个内接正方形ODFE和正方形FHCG如图所示,求c的值.
如图y=-x2+c与x轴相交于A,B两点,顶点C在y轴上,若该抛物线的两个内接正方形ODFE和正方形FHCG如图所示,求c的值.考点:抛物线与x轴的交点
专题:
分析:设出D、H的坐标,把D、H代入抛物线解析式,可得到方程组,求解即可求出c的值.
解答:解:∵四边形ODFE和四边形FHCG都是正方形,
∴设D坐标为(a,a),
则OF=2a,
设H为(b,b+2a),
∴CF=2b,则OC=2a+2b,
又∵D、H在抛物线y=-x2+c上,
代入可得
,
解得
,
∴c=6.
∴设D坐标为(a,a),
则OF=2a,
设H为(b,b+2a),
∴CF=2b,则OC=2a+2b,
又∵D、H在抛物线y=-x2+c上,
代入可得
|
解得
|
∴c=6.
点评:本题主要考查待定系数法求函数解析式及正方形的性质,结合正方形的性质找到c与两正方形的边长之间的关系是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
在
,
,
,-
,3.
,3.1415,2.010101…(相邻两个1之间有1个0)中,无理数有( )
| 25 |
| 2 |
| 11 |
| 3 |
| π |
| 3 |
| •• |
| 25 |
| A、1个 | B、2个 | C、3个 | D、4个 |
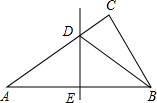 如图,在△ABC中,∠C=90°,DE垂直平分AB交AC于点D,垂足为E.
如图,在△ABC中,∠C=90°,DE垂直平分AB交AC于点D,垂足为E. 一游泳池长90米,甲、乙两人分别在游泳池相对两边同时朝另一边游泳,甲的速度是3米/秒,乙的速度是2米/秒,图中的实线和虚线分别为甲、乙与游泳池一边的距离随游泳时间的变化而变化的图象,若不计转向时间,则从开始起到3分钟止他们相遇的次数为
一游泳池长90米,甲、乙两人分别在游泳池相对两边同时朝另一边游泳,甲的速度是3米/秒,乙的速度是2米/秒,图中的实线和虚线分别为甲、乙与游泳池一边的距离随游泳时间的变化而变化的图象,若不计转向时间,则从开始起到3分钟止他们相遇的次数为 如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为E,F是BC中点,探究BD与EF的关系.并说明理由.
如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为E,F是BC中点,探究BD与EF的关系.并说明理由.