题目内容
观察下列算式
152=1×2×100+25=225
252=2×3×100+25=625
352=3×4×100+25=1225
…
(1)根据上面的算式,你发现了什么规律,请将规律用文字或字母表示出来;
(2)请对发现的规律进行证明;
(3)请利用发现的规律计算994×996.
152=1×2×100+25=225
252=2×3×100+25=625
352=3×4×100+25=1225
…
(1)根据上面的算式,你发现了什么规律,请将规律用文字或字母表示出来;
(2)请对发现的规律进行证明;
(3)请利用发现的规律计算994×996.
考点:规律型:数字的变化类
专题:
分析:(1)通过观察可以看出,个位是5的平方数,得数是100×去掉个位上的5剩下的数×(去掉个位上的5剩下的数+1)+25;得出:(10n+5)2=100×n×(n+1)+25;
(2)验证(1)中结论左右是否相等,只要把上面的结论的左边去掉括号化简看看是否等于右边即可判断;
(3)把994×996=9952-1,利用规律计算即可得出结果.
(2)验证(1)中结论左右是否相等,只要把上面的结论的左边去掉括号化简看看是否等于右边即可判断;
(3)把994×996=9952-1,利用规律计算即可得出结果.
解答:解:(1)(10n+5)2=100×n×(n+1)+25;
(2)左边=100n2+2×10n×5+52=100n2+100n+25,
右边=100n2+100n+25,
所以,左边=右边,因此结论正确;
(3)994×996
=9952-1
=100×992+100×99+25-1
=980100+9900+25-1
=990024.
(2)左边=100n2+2×10n×5+52=100n2+100n+25,
右边=100n2+100n+25,
所以,左边=右边,因此结论正确;
(3)994×996
=9952-1
=100×992+100×99+25-1
=980100+9900+25-1
=990024.
点评:此题考查数字的变化规律,从简单情形考虑,找出一般规律,利用规律解决问题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
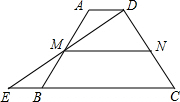 如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M
如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M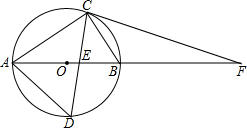 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,⊙O是△ABC的外接圆,∠ACB的平分线分别交⊙O、AB于点D、E,延长AB使PC=PE.
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,⊙O是△ABC的外接圆,∠ACB的平分线分别交⊙O、AB于点D、E,延长AB使PC=PE. 如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为E,F是BC中点,探究BD与EF的关系.并说明理由.
如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为E,F是BC中点,探究BD与EF的关系.并说明理由. 如图所示是一个边长为5cm的正六边形,如果要剪一张图形纸片完全盖住这个图形,那么这张图形纸片的半径最小应为多少?
如图所示是一个边长为5cm的正六边形,如果要剪一张图形纸片完全盖住这个图形,那么这张图形纸片的半径最小应为多少? A、B、C都在格点上,且每个小正方的边长都为1.已知AC=5,求B到直线AC的垂线段距离.
A、B、C都在格点上,且每个小正方的边长都为1.已知AC=5,求B到直线AC的垂线段距离.