题目内容
已知二次函数y=ax2+bx+c(a≠0)的图象顶点在第二象限,且经过点A(2,0)和B(0,2),则w=4a-2b+c的值的变化范围是 .
考点:二次函数图象与系数的关系
专题:
分析:将已知两点坐标代入二次函数解析式,得出c的值及a、b的关系式,代入w=4a-2b+c中消元,再根据对称轴的位置判断w的取值范围即可.
解答: 解:∵二次函数y=ax2+bx+c的顶点在第二象限,
解:∵二次函数y=ax2+bx+c的顶点在第二象限,
且过(0,2)和(2,0)分别代入抛物线解析式,
得c=2,4a+2b+2=0,
∴b=-2a-1,4a=-2b-2,
∵a<0,b<0,
∴由4a=-2b-2<0得到b>-1,结合上面b<0,所以-1<b<0①,
由b=-2a-1<0得到a>-
,结合上面a<0,所以-
<a<0②,
∴由①②得:-2<4a-2b<2,
得到0<4a-2b+2<4,
∴0<W<4.
故本题答案为:0<W<4.
 解:∵二次函数y=ax2+bx+c的顶点在第二象限,
解:∵二次函数y=ax2+bx+c的顶点在第二象限,且过(0,2)和(2,0)分别代入抛物线解析式,
得c=2,4a+2b+2=0,
∴b=-2a-1,4a=-2b-2,
∵a<0,b<0,
∴由4a=-2b-2<0得到b>-1,结合上面b<0,所以-1<b<0①,
由b=-2a-1<0得到a>-
| 1 |
| 2 |
| 1 |
| 2 |
∴由①②得:-2<4a-2b<2,
得到0<4a-2b+2<4,
∴0<W<4.
故本题答案为:0<W<4.
点评:本题考查了点与函数的关系,解题的关键是画草图,利用数形结合思想解题.

练习册系列答案
相关题目
 一游泳池长90米,甲、乙两人分别在游泳池相对两边同时朝另一边游泳,甲的速度是3米/秒,乙的速度是2米/秒,图中的实线和虚线分别为甲、乙与游泳池一边的距离随游泳时间的变化而变化的图象,若不计转向时间,则从开始起到3分钟止他们相遇的次数为
一游泳池长90米,甲、乙两人分别在游泳池相对两边同时朝另一边游泳,甲的速度是3米/秒,乙的速度是2米/秒,图中的实线和虚线分别为甲、乙与游泳池一边的距离随游泳时间的变化而变化的图象,若不计转向时间,则从开始起到3分钟止他们相遇的次数为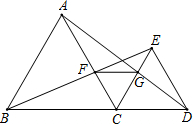 如图,已知点C在线段BD上,在BD的同侧作正△CDE、正△ABC,AC交BE于F,AD交CE于G,连接FG,在这个图形中,不在标注其它字母和添加任何辅助线,由这些条件可推出哪些结论?
如图,已知点C在线段BD上,在BD的同侧作正△CDE、正△ABC,AC交BE于F,AD交CE于G,连接FG,在这个图形中,不在标注其它字母和添加任何辅助线,由这些条件可推出哪些结论?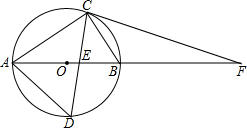 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,⊙O是△ABC的外接圆,∠ACB的平分线分别交⊙O、AB于点D、E,延长AB使PC=PE.
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,⊙O是△ABC的外接圆,∠ACB的平分线分别交⊙O、AB于点D、E,延长AB使PC=PE. 如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为E,F是BC中点,探究BD与EF的关系.并说明理由.
如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为E,F是BC中点,探究BD与EF的关系.并说明理由. 如图,等边△ABC中,D、E分别在AB、BC边上,且AD=2BE=4,连接DE,并将线段DE绕点E顺时针旋转60°,得到线段EF,连接CF,取EF中点G,连接AG,延长CF交AG于点H.若AH=
如图,等边△ABC中,D、E分别在AB、BC边上,且AD=2BE=4,连接DE,并将线段DE绕点E顺时针旋转60°,得到线段EF,连接CF,取EF中点G,连接AG,延长CF交AG于点H.若AH=