题目内容
如图，△ABC的中线AE，BD相交于点G，DF∥BC交AE于点F，求| FG |
| AE |
考点：三角形的重心,平行线分线段成比例
专题：
分析：首先证明AG=2GE，进而证明EG=2FG，即可解决问题．
解答：解：∵△ABC的中线AE，BD相交于点G，
∴AG=2GE，BG=2DG；
∵DF∥BC，
∴EG：FG=BG：DG=2，
∴EG=2FG；
∴AG=4FG，AE=6FG，
∴
=
=
，
即
的值为
．
解：∵△ABC的中线AE，BD相交于点G，∴AG=2GE，BG=2DG；
∵DF∥BC，
∴EG：FG=BG：DG=2，
∴EG=2FG；
∴AG=4FG，AE=6FG，
∴
| FG |
| AE |
| FG |
| 6FG |
| 1 |
| 6 |
即
| FG |
| AE |
| 1 |
| 6 |
点评：该题主要考查了三角形的重心的性质、平行线分线段成比例定理等几何知识点及其应用问题；解题的关键是牢固掌握定理内容，灵活运用定理来分析、判断、推理或解答．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
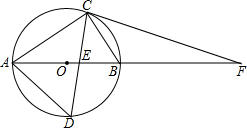如图，在Rt△ABC中，∠ACB=90°，AC=8cm，BC=6cm，⊙O是△ABC的外接圆，∠ACB的平分线分别交⊙O、AB于点D、E，延长AB使PC=PE．
如图，在△ABC中，D是AB上一点，AD=AC，AE⊥CD，垂足为E，F是BC中点，探究BD与EF的关系．并说明理由．
如图所示是一个边长为5cm的正六边形，如果要剪一张图形纸片完全盖住这个图形，那么这张图形纸片的半径最小应为多少？
如图，等边△ABC中，D、E分别在AB、BC边上，且AD=2BE=4，连接DE，并将线段DE绕点E顺时针旋转60°，得到线段EF，连接CF，取EF中点G，连接AG，延长CF交AG于点H．若AH=
如图，一个边长为4cm的等边三角形ABC与⊙O等高，⊙O与BC相切于点C，⊙O与AC相交于点D，则阴影部分的面积为
如图，OM、ON、OP分别是∠AOB、∠BOC、∠AOC的平分线，则∠AOP与∠MON的大小上有何关系？请你写出你的推测，并简要说明理由．