题目内容
1.已知,在△ABC中,AB=2,∠A=30°,BC=$\sqrt{2}$,则∠ABC=105°.分析 根据在△ABC中,AB=2,∠A=30°,BC=$\sqrt{2}$,由正弦定理可得∠C的值,从而可以求得本题的答案.
解答 解:∵在△ABC中,AB=2,∠A=30°,BC=$\sqrt{2}$,
∴$\frac{BC}{sinA}=\frac{AB}{sinC}$
即$\frac{\sqrt{2}}{\frac{1}{2}}=\frac{2}{sinC}$
解得sinC=$\frac{\sqrt{2}}{2}$
得∠C=45°
∴∠ABC=180°-∠A-∠C=180°-30°-45°=105°.
故答案为:105°.
点评 本题考查解直角三角形,关键是明确正弦定理的内容,找出求问题需要的条件.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
3.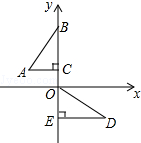 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )
 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )| A. | △ABC绕点C逆时针旋转90°,再向下平移2 | |
| B. | △ABC绕点C顺时针旋转90°,再向下平移2 | |
| C. | △ABC绕点C顺时针旋转90°,再向下平移6 | |
| D. | △ABC绕点C逆时针旋转90°,再向下平移6 |
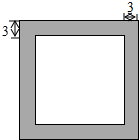 一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3米的正方形框(如图所示中阴影部分)已知铺这个框恰好用了192块边长为0.75米的正方形花岗石(接缝忽略不计),问标志性建筑底面的边长是多少米?
一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3米的正方形框(如图所示中阴影部分)已知铺这个框恰好用了192块边长为0.75米的正方形花岗石(接缝忽略不计),问标志性建筑底面的边长是多少米?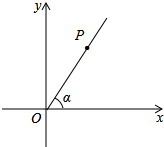 如图,点P是∠α的边OA上的一点,已知点P的横坐标为6,若sinα=$\frac{4}{5}$
如图,点P是∠α的边OA上的一点,已知点P的横坐标为6,若sinα=$\frac{4}{5}$