题目内容
9.(1)若(m+1)x<m+1的解集是x>1,则化简$\sqrt{(m-1)^{2}}$得1-m,m-1(2)若关于x的方程x-3k+2=0的解是正数,则k的取值范围为k<$\frac{2}{3}$.
分析 (1)根据不等式的性质,可得m的取值范围,根据二次根式的性质,可得答案;
(2)根据方程的解为正数,可得关于k的不等式,根据解不等式,可得答案.
解答 解:(1)由(m+1)x<m+1的解集是x>1,得
m+1>0,解得m>-1.
当-1<m<1时,$\sqrt{(m-1)^{2}}$=$\sqrt{(1-m)^{2}}$=1-m;
当m≥1时,$\sqrt{(m-1)^{2}}$=m-1;
故答案为:1-m,m-1;
(2)解x-3k+2=0,得x=2-3k.
由关于x的方程x-3k+2=0的解是正数,得
2-3k>0.
解得k<$\frac{2}{3}$,
故答案为:k<$\frac{2}{3}$.
点评 本题考查了二次根式的性质与化简,利用了不等式的性质,二次根式的性质:$\sqrt{{a}^{2}}$=$\left\{\begin{array}{l}{a(a≥0)}\\{-a(a<0)}\end{array}\right.$.

练习册系列答案
相关题目
18.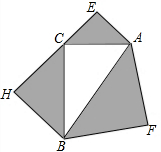 如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
 如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )| A. | 130 | B. | 120 | C. | 100 | D. | 90 |
 按下列要求作图.
按下列要求作图.
 如图,∠AOB=55°,画出∠BOC的平分线OD,计算∠AOD的度数.
如图,∠AOB=55°,画出∠BOC的平分线OD,计算∠AOD的度数.