题目内容
10.已知m、n、p为常数,若m+n+p=0,且m>n>p,在如下结论中:(1)m>0,p<0;
(2)关于x的方程nx+m+p=0一定是一元一次方程;
(3)m2016=(n+p)2016;
(4)$\frac{|m|}{m}$+$\frac{|n|}{n}$+$\frac{|p|}{p}$+$\frac{|mp|}{mp}$ 的值为0或-2;
(5)在数轴上点M、N、P表示数m、n、p,则OM=ON+OP或OP=ON+OM;
(6)关于x的方程nx=3-mx-px有无数个解.
正确结论的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据有理数的性质可对(1)进行判断;利用反例对(2)进行判断;根据乘方的意义对(3)进行判断;根据绝对值的意义对(4)进行判断;根据绝对值的几何意义对(5)进行判断;根据不定方程的解法对(6)进行判断.
解答 解:(1)因为m+n+p=0,则m、n、p中一定有一个正数和一个负数,所以m>0,p<0,所以(1)正确;
(2)若m=1,n=0,p=-1,则nx+m+p=0不是一元一次方程,所以(2)错误;
(3)因为m=-(n+p),所以m2016=(n+p)2016,所以(3)正确;
(4)|m|=m,|p|=-p,|pm|=-pm,所以$\frac{|m|}{m}$+$\frac{|n|}{n}$+$\frac{|p|}{p}$+$\frac{|mp|}{mp}$=$\frac{|n|}{n}$-1,所以代数式的值为0或-2,所以(4)正确;
(5)在数轴上点M、N、P表示数m、n、p,所以OM=m,ON=|n|,OP=-p,当n≤0时,OM=ON+OP,当n>0,OP=ON+OM,所以(5)正确;
(6)方程nx=3-mx-px整理为x(m+n+p)=3,而m+n+p=0,所以此方程没有解,所以(6)错误.
故选C.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.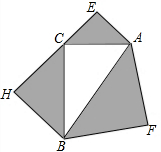 如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
 如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )| A. | 130 | B. | 120 | C. | 100 | D. | 90 |

 如图,∠AOB=55°,画出∠BOC的平分线OD,计算∠AOD的度数.
如图,∠AOB=55°,画出∠BOC的平分线OD,计算∠AOD的度数. 如图,一束光线从点A(3,4)出发,经过y轴上点(0,1)反射后经过点B(1,0),则光线从点A到点B经过的路径长为4$\sqrt{2}$.
如图,一束光线从点A(3,4)出发,经过y轴上点(0,1)反射后经过点B(1,0),则光线从点A到点B经过的路径长为4$\sqrt{2}$.