题目内容
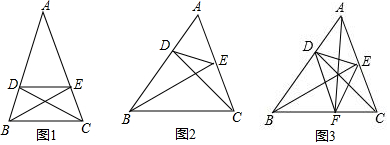
9. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其中部分图象如图所示,下列结论错误的是( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其中部分图象如图所示,下列结论错误的是( )| A. | 4ac<b2 | |
| B. | 方程ax2+bx+c=0的两个根是x1=-1,x2=3; | |
| C. | 当y>0时,x的取值范围是-1≤x<3 | |
| D. | 当x<0时,y随x增大而增大 |
分析 根据抛物线与x轴的交点情况、二次函数与方程的关系、二次函数的性质判断即可.
解答 解:∵抛物线与x轴有两个交点,
∴b2-4ac>0,
∴4ac<b2,A正确,不符合题意;
∵抛物线与x轴的一个交点是(-1,0),对称轴是x=1,
∴抛物线与x轴的另一个交点是(3,0),
∴方程ax2+bx+c=0的两个根是x1=-1,x2=3,B正确,不符合题意;
当y>0时,x的取值范围是-1<x<3,C错误,符合题意;
∵抛物线的对称轴是x=1,开口向下,
∴当x<0时,y随x增大而增大,D正确,不符合题意,
故选:C.
点评 本题考查的是抛物线与x轴的交点、二次函数图象与系数的关系以及二次函数与方程的关系,掌握二次函数的性质、二次函数图象与系数的关系是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
17.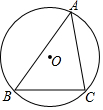 如图,点 O是△ABC外接圆的圆心,若⊙O的半径为5,∠A=45°,则$\widehat{BC}$的长是( )
如图,点 O是△ABC外接圆的圆心,若⊙O的半径为5,∠A=45°,则$\widehat{BC}$的长是( )
 如图,点 O是△ABC外接圆的圆心,若⊙O的半径为5,∠A=45°,则$\widehat{BC}$的长是( )
如图,点 O是△ABC外接圆的圆心,若⊙O的半径为5,∠A=45°,则$\widehat{BC}$的长是( )| A. | $\frac{5}{8}$π | B. | $\frac{25}{4}$π | C. | $\frac{5}{4}$π | D. | $\frac{5}{2}$π |
4.下列计算结果等于a5的是( )
| A. | a3+a2 | B. | a3•a2 | C. | (a3)2 | D. | a10÷a2 |
14.关于x的一元二次方程ax2-3x+3=0有两个不等实根,则a的取值范围是( )
| A. | a<$\frac{3}{4}$且a≠0 | B. | a>-$\frac{3}{4}$且a≠0 | C. | a>-$\frac{3}{4}$ | D. | a<$\frac{3}{4}$ |
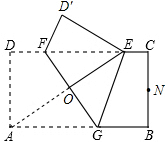 如图,矩形纸片ABCD中,AD=1,AB=2.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.当△AED的外接圆与BC相切于BC的中点N.则折痕FG的长为$\frac{17}{15}$.
如图,矩形纸片ABCD中,AD=1,AB=2.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.当△AED的外接圆与BC相切于BC的中点N.则折痕FG的长为$\frac{17}{15}$. 如图,已知AB为⊙O直径,过⊙O上一点C作⊙O的切线,交AB延长线于点E,作AD⊥CE,交EC延长线于D,交⊙O于点F,设∠ABC=α(0°<α<90°).
如图,已知AB为⊙O直径,过⊙O上一点C作⊙O的切线,交AB延长线于点E,作AD⊥CE,交EC延长线于D,交⊙O于点F,设∠ABC=α(0°<α<90°).