题目内容
17．
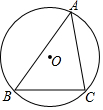如图，点 O是△ABC外接圆的圆心，若⊙O的半径为5，∠A=45°，则$\widehat{BC}$的长是（ ）| A． | $\frac{5}{8}$π | B． | $\frac{25}{4}$π | C． | $\frac{5}{4}$π | D． | $\frac{5}{2}$π |
分析 连接OB、OC，如图，先利用圆周角定理得到∠BOC=2∠A=90°，然后利用弧长公式求解．
解答 解：连接OB、OC，如图，
∠BOC=2∠A=90°，
所以$\widehat{BC}$的长=$\frac{90•π•5}{180}$=$\frac{5}{2}$π．
故选D．
点评 本题考查了弧长的计算：记住弧长公式：l=$\frac{n•π•R}{180}$（弧长为l，圆心角度数为n，圆的半径为R）．也考查了圆周角定理．
练习册系列答案
智慧小复习系列答案
相关题目
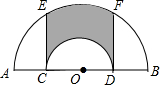如图，在半圆AOB中，点C为半径OA的中点，以O为圆心，OC为半径画半圆交OB于点D，分别过点C、D作CE、DF垂直AB，交圆O于点E、F，若OA=2，则阴影部分的面积为$\frac{3π}{2}$．
5．
如图，在正方形ABCD中，AB=6，分别以A、B、C、D为圆心，以正方形的边长为半径画弧，弧的交点设为E，F，G，H，则图中阴影部分的面积是$\frac{3+π-3\sqrt{3}}{3}$a2．
如图，在正方形ABCD中，AB=6，分别以A、B、C、D为圆心，以正方形的边长为半径画弧，弧的交点设为E，F，G，H，则图中阴影部分的面积是$\frac{3+π-3\sqrt{3}}{3}$a2． 
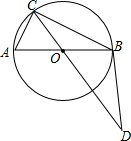如图，AB是⊙O的直径，C为⊙O上一点，点D在CO的延长线上，连接BD，已知BC=BD，AB=4，BC=2$\sqrt{3}$．
9．
如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（-1，0），其中部分图象如图所示，下列结论错误的是（ ）
如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（-1，0），其中部分图象如图所示，下列结论错误的是（ ）| A． | 4ac＜b2 | |
| B． | 方程ax2+bx+c=0的两个根是x1=-1，x2=3； | |
| C． | 当y＞0时，x的取值范围是-1≤x＜3 | |
| D． | 当x＜0时，y随x增大而增大 |
6．下面各数中，比-1大的数是（ ）
| A． | -5 | B． | -$\frac{3}{2}$ | C． | -2 | D． | -$\frac{1}{2}$ |
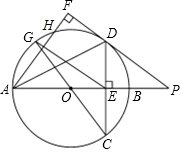如图，在⊙O中，直径AB垂直弦CD于E，过点D作弦AH的垂线，垂足为F，交AB的延长线于点P．