题目内容
13．一个口袋中装有四个完全相同的小球，把它们分别标号为1、2、3、4，随机摸出两个球，则摸出两个小球标号的和等于5的概率是$\frac{1}{3}$．分析 根据题意列出相应的表格，得出所有等可能的情况数，找出之和为5的情况数，即可求出所求的概率．
解答 解：列表得：
| 1 | 2 | 3 | 4 | |
| 1 | --- | （2，1） | （3，1） | （4，1） |
| 2 | （1，2） | --- | （3，2） | （4，2） |
| 3 | （1，3） | （2，3） | --- | （4，3） |
| 4 | （1，4） | （2，4） | （3，4） | --- |
∴摸出两个小球标号的和等于5的$\frac{4}{12}$=$\frac{1}{3}$，
故答案为：$\frac{1}{3}$．
点评 此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
如图，是一个几何体的三视图，由图中数据计算此几何体的表面积为28π（结果保留π）．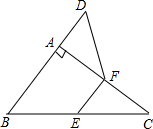
如图，在△ABC中，∠BAC=90°，延长BA到点D，使AD=$\frac{1}{2}$AB，E，F分别是边BC，AC的中点，试猜想DF与EC的数量关系，并证明你的猜想．
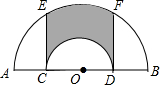如图，在半圆AOB中，点C为半径OA的中点，以O为圆心，OC为半径画半圆交OB于点D，分别过点C、D作CE、DF垂直AB，交圆O于点E、F，若OA=2，则阴影部分的面积为$\frac{3π}{2}$．
9．
如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（-1，0），其中部分图象如图所示，下列结论错误的是（ ）
如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（-1，0），其中部分图象如图所示，下列结论错误的是（ ）| A． | 4ac＜b2 | |
| B． | 方程ax2+bx+c=0的两个根是x1=-1，x2=3； | |
| C． | 当y＞0时，x的取值范围是-1≤x＜3 | |
| D． | 当x＜0时，y随x增大而增大 |