题目内容
19．已知直线y1=2x-4与双曲线y2=$\frac{k}{x}$（k＞0）在第一象限内交于点P（6，8），则当0＜y1＜y2时，自变量x的取值范围是2＜x＜6．分析 根据一次函数图象上点的坐标特征可求出直线y1=2x-4与x轴的交点，依照题意画出函数图象，根据两函数图象的上下位置关系可得出：当0＜x＜6时，y1＜y2，结合当x＞2时，0＜y1，即可得出当0＜y1＜y2时，自变量x的取值范围．
解答 解：当y1=2x-4=0时，x=2，
∴直线y1=2x-4与x轴的交点为（2，0）．
依照题意画出图形，如图所示．
观察函数图象可知：当0＜x＜6时，反比例函数图象在直线的上方，
∴当0＜x＜6时，y1＜y2．
又∵当x＞2时，0＜y1，
∴当0＜y1＜y2时，自变量x的取值范围是2＜x＜6．
故答案为：2＜x＜6．
点评 本题考查了反比例函数与一次函数的交点问题以及一次函数图象上点的坐标特征，依照题意画出函数图象，利用数形结合解决问题是解题的关键．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
9．
如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（-1，0），其中部分图象如图所示，下列结论错误的是（ ）
如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（-1，0），其中部分图象如图所示，下列结论错误的是（ ）| A． | 4ac＜b2 | |
| B． | 方程ax2+bx+c=0的两个根是x1=-1，x2=3； | |
| C． | 当y＞0时，x的取值范围是-1≤x＜3 | |
| D． | 当x＜0时，y随x增大而增大 |
10．某企业今年2月份产值为a万元，3月份比2月份增加了15%，4月份比3月份减少了5%，则4月份的产值为（ ）
| A． | （a+15%）（a-15%）万元 | B． | a（1+85%）（1-95%）万元 | C． | a（1+15%）（1-5%）万元 | D． | a（1+15%-5%）万元 |
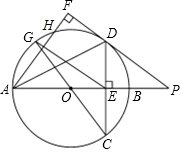如图，在⊙O中，直径AB垂直弦CD于E，过点D作弦AH的垂线，垂足为F，交AB的延长线于点P．
14．$\root{3}{64}$的算术平方根是（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | 4 | D． | ±2 |
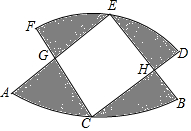如图，两个半径相等的直角扇形的圆心分别在对方的圆弧上，半径AE、CF交于点G，半径BE、CD交于点H，且点C是$\widehat{AB}$的中点，若扇形的半径为3，则图中阴影部分的面积等于$\frac{9π}{2}$-9．
11．下列等式一定成立的是（ ）
| A． | a2+a2=a5 | B． | （a-1）2=a2-1 | C． | （-a）9÷（-a）3=a6 | D． | （-2a2）3=8a6 |
8．下列图形中，不是中心对称图形的是（ ）
| A． | 平行四边形 | B． | 圆 | C． | 等边三角形 | D． | 正六边形 |