题目内容
9.先化简,再求值:$\frac{{a}^{2}-{b}^{2}}{a}$÷(a-$\frac{2ab-{b}^{2}}{a}$),其中a=$\sqrt{3}$+1,b=1-$\sqrt{3}$.分析 首先将括号里面分式进行通分进而分解因式,再化简把已知数据代入即可.
解答 解:原式=$\frac{(a+b)(a-b)}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{(a+b)(a-b)}{a}$×$\frac{a}{(a-b)^{2}}$
=$\frac{a+b}{a-b}$,
把a=$\sqrt{3}$+1,b=1-$\sqrt{3}$代入得:
原式=$\frac{\sqrt{3}+1+1-\sqrt{3}}{\sqrt{3}+1-(1-\sqrt{3})}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
点评 此题主要考查了分式的化简求值以及二次根式的化简求值,正确化简分式是解题关键.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
19.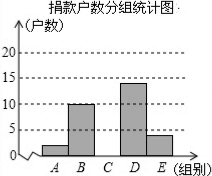 为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).
为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).
捐款户数分组统计表
请结合以上信息解答下列问题.
(1)a=0.28,本次调查样本的容量是50;
(2)先求出C组的户数为20户,再补全“捐款户数分组统计图”;
(3)直接写出捐款额的中位数落在C组.
 为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).
为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).捐款户数分组统计表
| 组别 | 捐款额(x)元 | 户数 | 频率 |
| A | 1≤x<100 | 2 | 0.04 |
| B | 100≤x<200 | 10 | 0.2 |
| C | 200≤x<300 | 0.4 | |
| D | 300≤x<400 | 14 | a |
| E | x≥400 | 4 | 0.08 |
(1)a=0.28,本次调查样本的容量是50;
(2)先求出C组的户数为20户,再补全“捐款户数分组统计图”;
(3)直接写出捐款额的中位数落在C组.
17.探究多边形内角和公式时,从n边形的一个顶点出发引出(n-3)条对角线,将n边形分割成(n-2)个三角形,这(n-2)个三角形的所有内角之和即为n边形的内角和,这一探究过程运用的数学思想是( )
| A. | 方程思想 | B. | 函数思想 | C. | 数形结合思想 | D. | 化归思想 |
4.直线l是以二元一次方程8x-4y=5的解为坐标所构成的直线,则该直线不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 △ABC的三个顶点坐标分别为A(2,-1),B(4,-2),C(1,-3),将△ABC平移至△A1B1C1的位置,点A、B、C对应的点分别为A1、B1、C1,已知点A1的坐标是(-2,3).
△ABC的三个顶点坐标分别为A(2,-1),B(4,-2),C(1,-3),将△ABC平移至△A1B1C1的位置,点A、B、C对应的点分别为A1、B1、C1,已知点A1的坐标是(-2,3). 如图,EF∥AD,∠1=∠2,试说明AB∥DG.
如图,EF∥AD,∠1=∠2,试说明AB∥DG.