题目内容
17．探究多边形内角和公式时，从n边形的一个顶点出发引出（n-3）条对角线，将n边形分割成（n-2）个三角形，这（n-2）个三角形的所有内角之和即为n边形的内角和，这一探究过程运用的数学思想是（ ）| A． | 方程思想 | B． | 函数思想 | C． | 数形结合思想 | D． | 化归思想 |
分析 根据题意即可得到结论．
解答 解：探究多边形内角和公式时，从n边形的一个顶点出发引出（n-3）条对角线，将n边形分割成（n-2）个三角形，这（n-2）个三角形的所有内角之和即为n边形的内角和，这一探究过程运用的数学思想是化归思想，
故选D．
点评 本题考查了多边形的内角和公式，数学思想，熟练掌握数学思想是解题的关键．
练习册系列答案
相关题目
8．下列二次根式，最简二次根式是（ ）
| A． | $\sqrt{\frac{1}{5}}$ | B． | $\sqrt{0.5}$ | C． | $\sqrt{5}$ | D． | $\sqrt{50}$ |
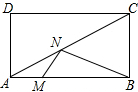如图，在矩形ABCD中，AB=4，AD=2，点M是AB上一动点，点N是对角线AC上一动点，则MN+BN的最小值为$\frac{16}{5}$．
2．下列四个图形中，不是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
7．
如图，已知直线a，b被直线c所截，则∠1和∠2是一对（ ）
如图，已知直线a，b被直线c所截，则∠1和∠2是一对（ ）| A． | 对顶角 | B． | 同位角 | C． | 内错角 | D． | 同旁内角 |