题目内容
20．解不等式组：$\left\{\begin{array}{l}{2x+1≥-1}\\{\frac{1+2x}{3}＞x-1}\end{array}\right.$，并把不等式组的解集在数轴上表示出来．分析 分别求出每一个不等式的解集，根据口诀：“大小小大中间找”确定不等式组的解集，再根据“大于向右，小于向左，包括端点用实心，不包括端点用空心”的原则在数轴上将解集表示出来．
解答 解：解不等式2x+1≥-1，得：x≥-1，
解不等式$\frac{1+2x}{3}$＞x-1，得：x＜4，
∴不等式组的解集为：-1≤x＜4，
将不等式解集表示在数轴上如下：
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
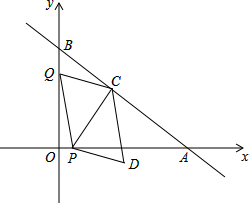如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（8，0），B（0，6），动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点Q从点B出发，沿射线BO方向以每秒2个单位的速度运动，过点P作PC⊥AB于点C，连接PQ，CQ，以PQ，CQ为邻边构造?PQCD，设点P运动的时间为t秒．
8．下列二次根式，最简二次根式是（ ）
| A． | $\sqrt{\frac{1}{5}}$ | B． | $\sqrt{0.5}$ | C． | $\sqrt{5}$ | D． | $\sqrt{50}$ |
已知命题“如果两条平行线被第三条直线所截，那么一对同位角的平分线互相平行”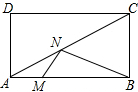
如图，在矩形ABCD中，AB=4，AD=2，点M是AB上一动点，点N是对角线AC上一动点，则MN+BN的最小值为$\frac{16}{5}$．
如图，D为等边三角形ABC内一点，AD=5，BD=6，CD=4，将△ABD绕A点逆时针旋转，使AB与AC重合，点D旋转至点E，连接DE．