题目内容
6. 如图,在矩形ABCD中,AB=8,AD=12,过A,D两点的⊙O与BC边相切于点E,则⊙O的半径为6.25.
如图,在矩形ABCD中,AB=8,AD=12,过A,D两点的⊙O与BC边相切于点E,则⊙O的半径为6.25.
分析 首先连接OE,并反向延长交AD于点F,连接OA,由在矩形ABCD中,过A,D两点的⊙O与BC边相切于点E,易得四边形CDFE是矩形,由垂径定理可求得AF的长,然后设⊙O的半径为x,则OE=EF-OE=8-x,利用勾股定理即可得:(8-x)2+36=x2,继而求得答案.
解答 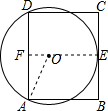 解:连接OE,并反向延长交AD于点F,连接OA,
解:连接OE,并反向延长交AD于点F,连接OA,
∵BC是切线,
∴OE⊥BC,
∴∠OEC=90°,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDFE是矩形,
∴EF=CD=AB=8,OF⊥AD,
∴AF=$\frac{1}{2}$AD=$\frac{1}{2}$×12=6,
设⊙O的半径为x,则OF=EF-OE=8-x,
在Rt△OAF中,OF2+AF2=OA2,
则(8-x)2+36=x2,
解得:x=6.25,
∴⊙O的半径为:6.25.
故答案为:6.25.
点评 此题考查了切线的性质、垂径定理、矩形的性质以及勾股定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
16.下列几种形状的瓷砖中,只用一种不能够铺满地面的是( )
| A. | 正三角形 | B. | 正四边形 | C. | 正五边形 | D. | 正六边形 |
1. 如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
 如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )| A. | BE=DF | B. | BF=DE | C. | AE=CF | D. | ∠1=∠2 |
11.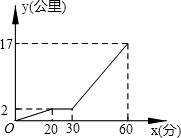 某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
 某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )| A. | 小强从家到公共汽车站步行了2公里 | |
| B. | 小强在公共汽车站等小明用了10分钟 | |
| C. | 公共汽车的平均速度是30公里/小时 | |
| D. | 小强乘公共汽车用了20分钟 |

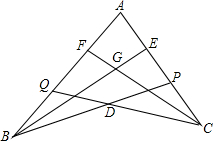 如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,求∠A的度数.
如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,求∠A的度数.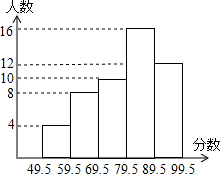 对某班学生一次数学测试成绩进行了统计(分数为整数),各分数段人数如图所示,则该班有学生20人,成绩在70.5~80.5
对某班学生一次数学测试成绩进行了统计(分数为整数),各分数段人数如图所示,则该班有学生20人,成绩在70.5~80.5