��Ŀ����
17��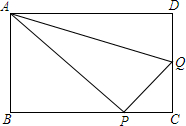 ��ͼ���ھ���ABCD�У�AB=6cm��BC=8cm������P��B�㿪ʼ�ر�BC���C��4cm/s���ٶ��˶���ͬʱ����Q��C�㿪ʼ�ر�CD���D��1cm/s���ٶ��˶���������һ�������յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶���
��ͼ���ھ���ABCD�У�AB=6cm��BC=8cm������P��B�㿪ʼ�ر�BC���C��4cm/s���ٶ��˶���ͬʱ����Q��C�㿪ʼ�ر�CD���D��1cm/s���ٶ��˶���������һ�������յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶�����1�����˶��������������PCQ������ﵽ$\frac{3}{2}$cm2��
��2�����˶�������������APQ�����Ϊy����д�����y��cm2�����˶�ʱ��t��s��֮��ĺ�����ϵʽ����д��t��ȡֵ��Χ��
��3����tΪ��ֵʱ��������APQ�������С������С����Ƕ���cm2��
���� ��1�����˶�x���������PCQ������ﵽ$\frac{3}{2}$cm2�����������ʾ��BP��CQ�����������ε������ʽ�г����̣��ⷽ�̼��ɣ�
��2������y=S�ı���ABCD-S��ABP-S��PCQ-S��ADQ����ͼ��ɣ�
��3�������䷽����һ��ʽ��Ϊ����ʽ�����ݶ��κ��������ʽ��
��� �⣺��1�����˶�x���������PCQ������ﵽ$\frac{3}{2}$cm2��
������ã�BP=4x��CQ=x��
��CP=8-4x��
��$\frac{1}{2}$����8-4x����x=$\frac{3}{2}$��
�����ã�4x2-8x+3=0��
��ã�x1=$\frac{3}{2}$��x2=$\frac{1}{2}$��
���˶�$\frac{3}{2}$��$\frac{1}{2}$���������PCQ������ﵽ$\frac{3}{2}$cm2��
��2��y=S�ı���ABCD-S��ABP-S��PCQ-S��ADQ
=48-$\frac{1}{2}$��4t��6-$\frac{1}{2}��$��8-4t����t-$\frac{1}{2}��$8����6-t��
=2t2-12t+24��0��t��2����
��3��y=2t2-12t+24=2��x-3��2+6��
��2��0��
��t��3ʱ��y��t���������С��
�൱t=2ʱ��������APQ�������С����С�����2��22-12��2+24=8cm2��
���� ���⿼����Ǿ��ε����ʡ���������ʽ���Ͷ��κ��������ʣ���������䷽�������ն��κ����������ǽ���Ĺؼ���

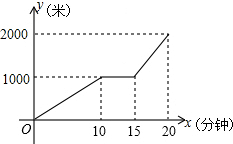 ij��С�������г��Ӽҳ���ȥѧУ��ѧ��;�������г��������ϣ���������һ��ʱ���������У���ʱ�ϵ���ѧУ����С������������ʱ��Ϊx�����ӣ�����ҵľ���Ϊy���ף���y��x�ĺ����Ĵ���ͼ����ͼ��ʾ������˵��������ǣ�������
ij��С�������г��Ӽҳ���ȥѧУ��ѧ��;�������г��������ϣ���������һ��ʱ���������У���ʱ�ϵ���ѧУ����С������������ʱ��Ϊx�����ӣ�����ҵľ���Ϊy���ף���y��x�ĺ����Ĵ���ͼ����ͼ��ʾ������˵��������ǣ�������| A�� | �ҵ�ѧУ�ľ�����2000�� | |
| B�� | �������ʱ����5���� | |
| C�� | �������г����ٶ���ÿ����200�� | |
| D�� | ��ǰ�������ٶȿ� |
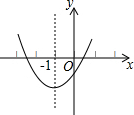 ��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����Գ���Ϊֱ��x=-1���������н��ۣ���1��abc��0����2��2a+b=0����3��a+b+c��0����4��a-b+c��0������ȷ�Ľ����ǣ�������
��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����Գ���Ϊֱ��x=-1���������н��ۣ���1��abc��0����2��2a+b=0����3��a+b+c��0����4��a-b+c��0������ȷ�Ľ����ǣ�������| A�� | ��l����2�� | B�� | ��2����3�� | C�� | ��2����4�� | D�� | ��3����4�� |
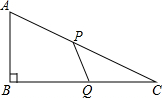 ��ͼ���ڡ�ABC�У���B=90�㣬AB=6�ף�BC=8�ף�����P��2��/����ٶȴ�A���������AC���C�ƶ���ͬʱ������Q��1��/����ٶȴ�C���������CB���B�ƶ�����������һ�㵽���յ�ʱ�����Ƕ�ֹͣ�����ƶ���ʱ��Ϊt�룮
��ͼ���ڡ�ABC�У���B=90�㣬AB=6�ף�BC=8�ף�����P��2��/����ٶȴ�A���������AC���C�ƶ���ͬʱ������Q��1��/����ٶȴ�C���������CB���B�ƶ�����������һ�㵽���յ�ʱ�����Ƕ�ֹͣ�����ƶ���ʱ��Ϊt�룮