题目内容
 如图,已知AD∥BC,M为AB的中点.
如图,已知AD∥BC,M为AB的中点.(1)过点M作MN∥AD交CD于点N.
(2)MN和BC平行吗?为什么?
考点:梯形中位线定理
专题:
分析:(1)根据题意画出图形即可;
(2)根据平行线的性质求出∠A+∠B=180°,∠A+∠AMN=180°,推出∠AMN=∠B,根据平行线的判定得出即可.
(2)根据平行线的性质求出∠A+∠B=180°,∠A+∠AMN=180°,推出∠AMN=∠B,根据平行线的判定得出即可.
解答:解:(1)如图所示:
 ;
;
(2)MN∥BC,
理由是:∵AD∥BC,
∴∠A+∠B=180°,
∵AD∥MN,
∴∠A+∠AMN=180°,
∴∠AMN=∠B,
∴MN∥BC.
 ;
;(2)MN∥BC,
理由是:∵AD∥BC,
∴∠A+∠B=180°,
∵AD∥MN,
∴∠A+∠AMN=180°,
∴∠AMN=∠B,
∴MN∥BC.
点评:本题考查了梯形的中位线,平行线的性质和判定的应用,能应用平行线的性质和判定定理进行推理是解此题的关键,难度适中.

练习册系列答案
相关题目
 如图,⊙O中,弦AB,CD相交于P点,连接AC,BD,则下列结论一定正确的是 ( )
如图,⊙O中,弦AB,CD相交于P点,连接AC,BD,则下列结论一定正确的是 ( )| A、∠A=∠B |
| B、∠C=∠D |
| C、PA:PB=PC:PD |
| D、PA:PD=PC:PB |
 如图,直线AB,CD相交于点O,∠EOA=90°,∠COE=
如图,直线AB,CD相交于点O,∠EOA=90°,∠COE=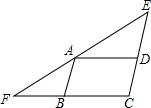 已知,如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB,AB=a,AD=b.
已知,如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB,AB=a,AD=b. 如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°
如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90° 已知直线l1:y=-
已知直线l1:y=- 如图,已知⊙O的半径R=4,点P是⊙O内的一定点,且OP=2,则过点P的直线与⊙O交于AB,则AB的最小值为
如图,已知⊙O的半径R=4,点P是⊙O内的一定点,且OP=2,则过点P的直线与⊙O交于AB,则AB的最小值为 如图所示,在平行四边形ABCD中,点E,F分别在AD,BC上,且BE∥DF,AC与EF相交于点O.证明:O为AC,EF的中点.
如图所示,在平行四边形ABCD中,点E,F分别在AD,BC上,且BE∥DF,AC与EF相交于点O.证明:O为AC,EF的中点.