题目内容
 如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°
如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°(1)求AO的长;
(2)求△BOC的周长;
(3)求四边形ABCD的周长;
(4)求AB边上的高.
考点:平行四边形的判定与性质,勾股定理,勾股定理的逆定理
专题:
分析:(1)由平行四边形的性质可知AO=
AC;
(2)由平行四边形的性质可得BC=AD,结合条件可求得△BOC的周长;
(3)在△ABD中可求得AB,进一步可求得四边形ABCD的周长;
(4)设AB边上的高为h,由面积相等可知AB•h=AD•BD,可求得h.
| 1 |
| 2 |
(2)由平行四边形的性质可得BC=AD,结合条件可求得△BOC的周长;
(3)在△ABD中可求得AB,进一步可求得四边形ABCD的周长;
(4)设AB边上的高为h,由面积相等可知AB•h=AD•BD,可求得h.
解答:解:(1)∵四边形ABCD为平行四边形,
∴AO=
AC=
×26=13;
(2)∵四边形ABCD为平行四边形,
∴BC=AD=12,CO=AO=13,
∴BC+BO+CO=12+13+5=30,
即△BOC的周长为30;
(3)∵∠ADB=90°,AD=12,BD=BO+DO=10,
∴在Rt△ABD中由勾股定理可得AB=
=
=2
,
∴四边形ABCD周长为2(AB+AD)=2×(2
+12)=4
+24;
(4)设AB边上的高为h,
则S四边形ABCD=AB•h=AD•BD,
即2
h=12×10,
解得h=
,
即AB边上的高为
.
∴AO=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵四边形ABCD为平行四边形,
∴BC=AD=12,CO=AO=13,
∴BC+BO+CO=12+13+5=30,
即△BOC的周长为30;
(3)∵∠ADB=90°,AD=12,BD=BO+DO=10,
∴在Rt△ABD中由勾股定理可得AB=
| AD2+BD2 |
| 122+102 |
| 61 |
∴四边形ABCD周长为2(AB+AD)=2×(2
| 61 |
| 61 |
(4)设AB边上的高为h,
则S四边形ABCD=AB•h=AD•BD,
即2
| 61 |
解得h=
60
| ||
| 61 |
即AB边上的高为
60
| ||
| 61 |
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
下列说法不正确的是( )
| A、等腰三角形两腰上的中线相等 |
| B、等腰三角形两底角平分线相等 |
| C、等腰三角形的高,中线,角平分线互相重合 |
| D、等边三角形的高,中线,角平分线互相重合 |
 如图,在直线MN上找点P,使点P到∠AOB两边的距离相等,符合条件的有( )个.
如图,在直线MN上找点P,使点P到∠AOB两边的距离相等,符合条件的有( )个.| A、0 | B、1 | C、2 | D、3 |
 根据二次函数y=ax2+bx+c的图象草图回答下列问题:
根据二次函数y=ax2+bx+c的图象草图回答下列问题: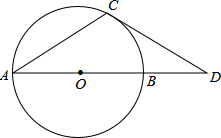 如图,点D在⊙O的直径AB的延长线上,点C在⊙C上,AC=CD,∠D=30°
如图,点D在⊙O的直径AB的延长线上,点C在⊙C上,AC=CD,∠D=30° 已知如图,∠3+∠5+∠7=200°,则∠1+∠2+∠4+∠6+∠8=
已知如图,∠3+∠5+∠7=200°,则∠1+∠2+∠4+∠6+∠8= 如图,已知AD∥BC,M为AB的中点.
如图,已知AD∥BC,M为AB的中点. 如图所示,AB是⊙O的一条直径,CD是⊙O的一条弦,延长BA与DC的延长线相交于P点,若AB=2PC,∠P=36°,求∠COD的度数.
如图所示,AB是⊙O的一条直径,CD是⊙O的一条弦,延长BA与DC的延长线相交于P点,若AB=2PC,∠P=36°,求∠COD的度数. 如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C分别在x轴的负半轴、y轴的正半轴上,已知A(-1,0)、D(2,3),并且二次函数y=ax2+bx+c的图象经过A、C、D三点.
如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C分别在x轴的负半轴、y轴的正半轴上,已知A(-1,0)、D(2,3),并且二次函数y=ax2+bx+c的图象经过A、C、D三点.