题目内容
11.先化简,在求值:($\frac{2-x}{x+2}$-x-1)÷$\frac{2x}{{x}^{2}-4}$,在2,-2,4,-4选取合适的x代入求值.分析 先算括号里面的,再算除法,最后选出合适的x的值代入进行计算即可.
解答 解:原式=$\frac{2-x-(x+1)(x+2)}{x+2}$•$\frac{(x+2)(x-2)}{2x}$
=$\frac{2-x-{x}^{2}-2x-x-2}{x+2}$•$\frac{(x+2)(x-2)}{2x}$
=$\frac{-{x}^{2}-4x}{x+2}$•$\frac{(x+2)(x-2)}{2x}$
=-$\frac{(x+4)(x-2)}{2}$,
当x=-4时,原式=0.
点评 本题考查的是分式的化简求值,在解答此类题目时要注意所选x的值要保证分式有意义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.下列各组条件中,能判断两个直角三角形全等的是( )
| A. | 一组边对应相等 | B. | 两组直角边对应相等 | ||
| C. | 两组锐角对应相等 | D. | 一组锐角对应相等 |
6.下列函数是一次函数的是( )
| A. | y=kx+2 | B. | y=-$\frac{6}{x}$ | C. | y=-3x2+2 | D. | y=-$\frac{x}{4}$ |
16.下列命题:
①圆上任意两点间的部分叫弦
②长度相等的弧叫等弧
③在同圆或等圆中相等的弦所对的弧相等
④平分弦的直径垂直于弦
⑤半圆或直径所对的圆周角是直角
正确的个数是( )个.
①圆上任意两点间的部分叫弦
②长度相等的弧叫等弧
③在同圆或等圆中相等的弦所对的弧相等
④平分弦的直径垂直于弦
⑤半圆或直径所对的圆周角是直角
正确的个数是( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.已知点O为△ABC的外心,若∠A=40°,则∠BOC的度数为( )
| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
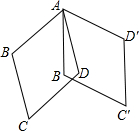 如图,菱形ABCD中,∠B=120°,AB=2,将图中的菱形ABCD绕点A沿逆时针方向旋转,得菱形AB′C′D′,若∠BAD′=110°,在旋转的过程中,点C经过的路线长为$\frac{{5\sqrt{3}}}{9}π$.
如图,菱形ABCD中,∠B=120°,AB=2,将图中的菱形ABCD绕点A沿逆时针方向旋转,得菱形AB′C′D′,若∠BAD′=110°,在旋转的过程中,点C经过的路线长为$\frac{{5\sqrt{3}}}{9}π$. 如图,AC与BD相交于点O,AO=DO,∠1=∠2,求证:AB=CD.
如图,AC与BD相交于点O,AO=DO,∠1=∠2,求证:AB=CD.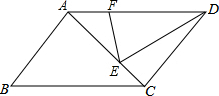 如图,在平行四边形ABCD中,E在AC上,AE=2EC,F在AD上,DF=2AF,如果△DEF的面积为2,则平行四边形ABCD的面积为( )
如图,在平行四边形ABCD中,E在AC上,AE=2EC,F在AD上,DF=2AF,如果△DEF的面积为2,则平行四边形ABCD的面积为( )