题目内容
1．
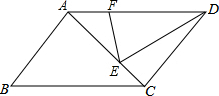如图，在平行四边形ABCD中，E在AC上，AE=2EC，F在AD上，DF=2AF，如果△DEF的面积为2，则平行四边形ABCD的面积为（ ）| A． | 4 | B． | 8 | C． | 9 | D． | 10 |
分析 由线段之间的关系分别得出几个小三角形的面积关系，进而可得出平行四边形的面积．
解答 解：∵DF=2AF，
∴DF=$\frac{2}{3}$AD，
∴$\frac{△ADE的面积}{△DEF的面积}$=$\frac{3}{2}$．
∴△ADE的面积=$\frac{3}{2}$×2=3，
又∵AE=2EC，
∴AC=$\frac{3}{2}$AE，
∴△ADC的面积=$\frac{3}{2}$△ADE的面积=$\frac{9}{2}$，
∴平行四边形ABCD的面积=2△ADC的面积=9．
故选：C．
点评 本题考查了平行四边形的性质、三角形的面积关系；熟练掌握平行四边形的性质，弄清几个小三角形的面积关系是解决问题的关键．
练习册系列答案
相关题目
9．若关于x的一元二次方程x2-2mx-m-$\frac{1}{4}$=0有两个相等的实数根，则m的值为（ ）
| A． | m=$\frac{1}{2}$ | B． | m=-$\frac{1}{2}$ | C． | m=2 | D． | m=-2 |
16．下列从左到右的变形中，属于因式分解的是（ ）
| A． | （x+y）（x-2y）=x2-x+y2 | B． | （a-b）2=（a-b）（a-b） | C． | 3x2-x=x（3x-1） | D． | m2-n2=（m-n）2 |
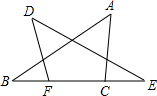如图，点F、C在BE上，BF=CE，∠A=∠D，∠B=∠E．
如图，若直线a∥b，那么∠x=64度．