题目内容
5. △ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )
△ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )| A. | 80° | B. | 90° | C. | 100° | D. | 110° |
分析 由题中条件可得∠B=∠BDE,∠C=∠CGF,进而再利用外角的性质及平行四边形邻角互补,即可得出结论.
解答 解:∵BE=DE,CF=FG,
∴∠B=∠BDE,∠C=∠CGF,
∠DEF=∠B+∠BDE=2∠B,则∠EFG=2∠C,
∵四边形DEFG是平行四边形,
∴∠DEF+∠EFG=180°,
∴$\frac{1}{2}$(∠DEF+∠EFG)=∠B+∠C=90°,
∴∠A=90°.
故选B.
点评 本题考查了相似三角形、平行四边形的性质以及三角形的内角和定理,应熟练掌握.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
16.方程$\frac{5}{{x}^{2}+x}$+$\frac{3}{{x}^{2}-x}$=$\frac{6}{{x}^{2}-1}$的解为( )
| A. | x=1 | B. | x=-1 | C. | x=$\frac{3}{5}$ | D. | 无解 |
20.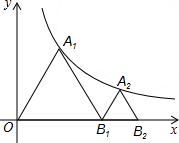 如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )
如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )
 如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )
如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )| A. | (4,0) | B. | (4$\sqrt{2}$,0) | C. | (6,0) | D. | (6$\sqrt{2}$,0) |
15.若关于x的一元二次方程(m+1)x2-2x+1=0有实数根,则实数m的取值范围是( )
| A. | m≥0 | B. | m≤0 | C. | m≠1 | D. | m≤0且m≠-1 |
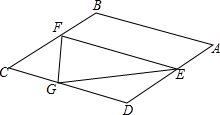 如图,在菱形ABCD中,AB=$\sqrt{3}$,∠B=120°,E是AD边上的一个动点(不与点A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.
如图,在菱形ABCD中,AB=$\sqrt{3}$,∠B=120°,E是AD边上的一个动点(不与点A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.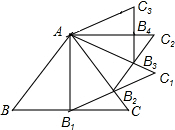 如图,等边△ABC的边长为2,以BC边上的高AB1为边作等边△AB1C1,B1C1交AC于点B2,△AB1B2的面积记做S1;再以AB2为边作等边△AB2C2,B2C2交AC1于点B3,△AB2B3的面积记做S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$..
如图,等边△ABC的边长为2,以BC边上的高AB1为边作等边△AB1C1,B1C1交AC于点B2,△AB1B2的面积记做S1;再以AB2为边作等边△AB2C2,B2C2交AC1于点B3,△AB2B3的面积记做S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$..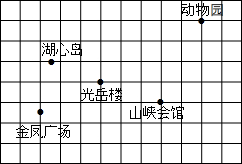 如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长都为1个单位长度).建立适当的平面直角坐标系,使光岳楼的坐标为(-1,0),并用坐标表示下列景点的位置.
如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长都为1个单位长度).建立适当的平面直角坐标系,使光岳楼的坐标为(-1,0),并用坐标表示下列景点的位置.