题目内容
下列图形中是轴对称而不是中心对称图形的是( )
A. 平行四边形
B. 线段
C. 角
D. 正方形
 C
【解析】试题解析:平行四边形的对称中心为两条对角线的交点,不是轴对称图形;线段的对称中心为线段的中点,对称轴为线段的中垂线;角不是中心对称图形,对称轴为角平分线所在直线;正方形的对称中心为两条对角线的交点,对称轴为两条对角线所在直线及两条对边中点连线所在直线;所以选择C.
C
【解析】试题解析:平行四边形的对称中心为两条对角线的交点,不是轴对称图形;线段的对称中心为线段的中点,对称轴为线段的中垂线;角不是中心对称图形,对称轴为角平分线所在直线;正方形的对称中心为两条对角线的交点,对称轴为两条对角线所在直线及两条对边中点连线所在直线;所以选择C.
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
我会连.(任意摸出一个球,可能是什么颜色?)



一定是白球 可能是白球 不可能是白球
 【解析】试题分析: 本题考察对可能性大小的应用,关键是推断出各袋子中能摸出的球的颜色的频率如何.
【解析】
因为三个袋子中所装的球的颜色是不同的,第一个袋子中全是黑球,第二是全是白球,第三个里面有黑球也有白球,所以,从第二个袋子中摸出的一定是白球,第一个袋子中摸出来的一定不是白球;第三个袋子中摸出来的可能是白球也可能是黑球.故连接如上图所示.
【解析】试题分析: 本题考察对可能性大小的应用,关键是推断出各袋子中能摸出的球的颜色的频率如何.
【解析】
因为三个袋子中所装的球的颜色是不同的,第一个袋子中全是黑球,第二是全是白球,第三个里面有黑球也有白球,所以,从第二个袋子中摸出的一定是白球,第一个袋子中摸出来的一定不是白球;第三个袋子中摸出来的可能是白球也可能是黑球.故连接如上图所示. 如图,点D在BC上,DE⊥AB,DF⊥AC,垂足分别为E、F,DE=DF.求证:AD垂直平分EF.
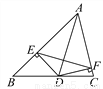
 见解析
【解析】试题分析:根据直角三角形的判定定理证明Rt△AED≌Rt△AFD,得到AE=AF,根据线段垂直平分线的判定定理证明结论.
试题解析:
在Rt△AED和Rt△AFD中,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
又∵DE=DF,
∴AD是EF的垂直平分线,即AD垂直平分EF.
见解析
【解析】试题分析:根据直角三角形的判定定理证明Rt△AED≌Rt△AFD,得到AE=AF,根据线段垂直平分线的判定定理证明结论.
试题解析:
在Rt△AED和Rt△AFD中,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
又∵DE=DF,
∴AD是EF的垂直平分线,即AD垂直平分EF. 关于点O成中心对称的两个四边形ABCD和DEFG,AD、BE、CF、DG都过______
 点O
【解析】对应点的连线经过对称中心.
故答案:点O.
点O
【解析】对应点的连线经过对称中心.
故答案:点O. 下列图形中,是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
 A
【解析】根据中心对称的定义可知只有A选项符合,故选A.
A
【解析】根据中心对称的定义可知只有A选项符合,故选A. 分解因式: 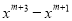 =____________________.
=____________________.
 xm+1(x+1)(x-1)
【解析】= xm+1(x2-1)= xm+1(x+1)(x-1),
故答案为:xm+1(x+1)(x-1).
xm+1(x+1)(x-1)
【解析】= xm+1(x2-1)= xm+1(x+1)(x-1),
故答案为:xm+1(x+1)(x-1). 在括号内填上适当的因式:
(1)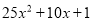 =(______); (2)
=(______); (2)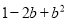 =(_____)
=(_____)
(3)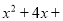 (_____)=(x+__)² (4)
(_____)=(x+__)² (4)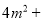 (____)+9n²=(_____)²
(____)+9n²=(_____)²
 (1)5x+1; (2)b-1 (3)4, 2 (4)±12mn; 2m±3n;
【解析】试题解析:(1)25x2+10x+1=(5x+1)2;
(2)1-2b+b2=(b-1)2
(3)x2+4x+4=(x+2)2;
(4)4m2+(±12mn)+9n2=(2m±3n)2.
故答案为:(5x+1),(b-1),4,2,±12mn,(2m±3n).
(1)5x+1; (2)b-1 (3)4, 2 (4)±12mn; 2m±3n;
【解析】试题解析:(1)25x2+10x+1=(5x+1)2;
(2)1-2b+b2=(b-1)2
(3)x2+4x+4=(x+2)2;
(4)4m2+(±12mn)+9n2=(2m±3n)2.
故答案为:(5x+1),(b-1),4,2,±12mn,(2m±3n). 下列各式中能用平方差公式分解因式的是( )
A. 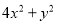 B.
B. 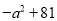 C.
C. 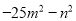 D.
D. 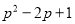
 B
【解析】A选项4x2+y2,符号相同,无法运用平方差公式分解因式,故此选项错误;B选项-a2+81,能运用平方差公式分解因式,故此选项正确;C选项-25m2-n2,符号相同,无法运用平方差公式分解因式,故此选项错误;D选项p2-2p+1,无法运用平方差公式分解因式,故此选项错误,
故选B.
B
【解析】A选项4x2+y2,符号相同,无法运用平方差公式分解因式,故此选项错误;B选项-a2+81,能运用平方差公式分解因式,故此选项正确;C选项-25m2-n2,符号相同,无法运用平方差公式分解因式,故此选项错误;D选项p2-2p+1,无法运用平方差公式分解因式,故此选项错误,
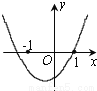
故选B. 已知函数y=(x-a)(x-b)(其中a>b)的图象如图所示,则函数y=ax+b的图象可能正确的是( )
A. 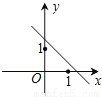 B.
B. 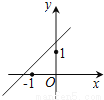 C.
C. 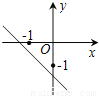 D.
D. 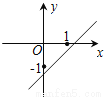
 D
【解析】根据图象可得出方程(x-a)(x-b)=0的两个实数根为a,b,且一正一负,负数的绝对值大,
∵a>b,∴a>0,b<0,
∴函数y=ax+b的图象经过第一、三、四象限,
故选:D.
D
【解析】根据图象可得出方程(x-a)(x-b)=0的两个实数根为a,b,且一正一负,负数的绝对值大,
∵a>b,∴a>0,b<0,
∴函数y=ax+b的图象经过第一、三、四象限,
故选:D. 
