��Ŀ����
��ͼ����֪ƽ���ı���ABCD��DE�ǡ�ADC�Ľ�ƽ���ߣ���BC�ڵ�E��
��1����֤��CD=CE��
��2����BE=CE����B=80�㣬���DAE�Ķ�����
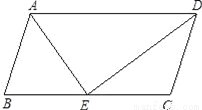
 ��1��֤������������2����DAE=50�㣮
���������������:��1������DE�ǡ�ADC�Ľ�ƽ���ߵõ���1=��2���ٸ���ƽ���ı��ε����ʵõ���1=��3�����ԡ�2=��3�����ݵȽǶԵȱ��ɵ�֤��
��2���ȸ���BE=CE���CD=CE�õ���ABE�ǵ��������Σ������BAE�Ķ������ٸ���ƽ���ı����ڽǻ����õ���BAD=100�㣬���ԡ�DAE����
��1��֤������ͼ����ƽ���ı���ABCD��...
��1��֤������������2����DAE=50�㣮
���������������:��1������DE�ǡ�ADC�Ľ�ƽ���ߵõ���1=��2���ٸ���ƽ���ı��ε����ʵõ���1=��3�����ԡ�2=��3�����ݵȽǶԵȱ��ɵ�֤��
��2���ȸ���BE=CE���CD=CE�õ���ABE�ǵ��������Σ������BAE�Ķ������ٸ���ƽ���ı����ڽǻ����õ���BAD=100�㣬���ԡ�DAE����
��1��֤������ͼ����ƽ���ı���ABCD��...
��ϰ��ϵ�д�
 ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д� ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
�����Ŀ
���в���ʽ������ȷ���ǣ� ��
A����a��b����a��2��b��2 B����a��b����|a|��|b|
C����a��b���é�2a����2b D����a��b����a2��b2
 C
��������
������������ݲ���ʽ���ӣ������ͬһ��������ʽ�ӣ������Ⱥŵķ��䣻��ʽ���߳ˣ�����ԣ�ͬһ�����������Ⱥŵķ��䣻����ʽ���߳ˣ�����ԣ�ͬһ�����������Ⱥŵķ���ı䣬�ɵã�
A����ʽ�����߶���2�����Ⱥŵķ��䣬��A����
B����a=2��b=��3��a��b����|a|��|b|����B����
C������ʽ�����߶����ԩ�2�����Ⱥŵķ���ı䣬��C��ȷ��
...
C
��������
������������ݲ���ʽ���ӣ������ͬһ��������ʽ�ӣ������Ⱥŵķ��䣻��ʽ���߳ˣ�����ԣ�ͬһ�����������Ⱥŵķ��䣻����ʽ���߳ˣ�����ԣ�ͬһ�����������Ⱥŵķ���ı䣬�ɵã�
A����ʽ�����߶���2�����Ⱥŵķ��䣬��A����
B����a=2��b=��3��a��b����|a|��|b|����B����
C������ʽ�����߶����ԩ�2�����Ⱥŵķ���ı䣬��C��ȷ��
... ��ʽ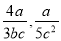 �����ĸ��_________��
�����ĸ��_________��
 15bc2
�������������������ʽ������ĸ��15bc2��
�ʴ�Ϊ��15bc2��
15bc2
�������������������ʽ������ĸ��15bc2��
�ʴ�Ϊ��15bc2�� ��ͼ��BC=4cm��AB=3cm��AF=12cm��AC��AF��������CDEF�������169cm2�����жϡ�ABC����״��
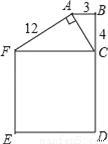
 ��ABC��ֱ��������.
�����������������ȸ��������ε�������FC�ij�������Rt��ACF�����ù��ɶ������AC�ij���Ȼ����ݹ��ɶ����涨��֤����B=90�㼴�ɣ�
���������
��������CDEF�������169 cm2��
��FC=13 cm
��Rt��ACF�У��ɹ��ɶ����ã�
AC2=CF2��AF2=132��122=25��
�ڡ�ABC�У���ΪAB2+BC2=32+...
��ABC��ֱ��������.
�����������������ȸ��������ε�������FC�ij�������Rt��ACF�����ù��ɶ������AC�ij���Ȼ����ݹ��ɶ����涨��֤����B=90�㼴�ɣ�
���������
��������CDEF�������169 cm2��
��FC=13 cm
��Rt��ACF�У��ɹ��ɶ����ã�
AC2=CF2��AF2=132��122=25��
�ڡ�ABC�У���ΪAB2+BC2=32+... ��Rt��ABC�У���C=90�㣬AC=9��BC=12�����C��AB�ľ����ǣ�������
A. 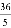 B.
B. 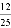 C.
C.  D.
D. 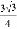
 A
��������������������ȸ��ݹ��ɶ����ɵã�AB=�����ݵ�������ɵã���C��AB�ľ���Ϊ��(9��12)��15=.
A
��������������������ȸ��ݹ��ɶ����ɵã�AB=�����ݵ�������ɵã���C��AB�ľ���Ϊ��(9��12)��15=. ��֪ƽ���ı���ABCD�У���B=4��A�����C=__��
 36��
��������������������ı���BCDA��ƽ���ı��Σ�
��AD��CB����A=��C��
���A+��B=180�㣬
�ߡ�B=4��A��
���A+4��A=180�㣬
��ã���A=36�㣬
���C=36��.
36��
��������������������ı���BCDA��ƽ���ı��Σ�
��AD��CB����A=��C��
���A+��B=180�㣬
�ߡ�B=4��A��
���A+4��A=180�㣬
��ã���A=36�㣬
���C=36��. �һ���.����������һ��������ʲô��ɫ����



һ���ǰ��� �����ǰ��� �������ǰ���
 ���������������: ���⿼��Կ����Դ�С��Ӧ�ã��ؼ����ƶϳ����������������������ɫ��Ƶ�����.
��������
��Ϊ������������װ�������ɫ�Dz�ͬ�ģ���һ��������ȫ�Ǻ��ڶ���ȫ�ǰ������������к���Ҳ�а������ԣ��ӵڶ���������������һ���ǰ���һ����������������һ�����ǰ��������������������Ŀ����ǰ���Ҳ�����Ǻ���.����������ͼ��ʾ.
���������������: ���⿼��Կ����Դ�С��Ӧ�ã��ؼ����ƶϳ����������������������ɫ��Ƶ�����.
��������
��Ϊ������������װ�������ɫ�Dz�ͬ�ģ���һ��������ȫ�Ǻ��ڶ���ȫ�ǰ������������к���Ҳ�а������ԣ��ӵڶ���������������һ���ǰ���һ����������������һ�����ǰ��������������������Ŀ����ǰ���Ҳ�����Ǻ���.����������ͼ��ʾ. һ���ڴ�����5������3������2������������һ���������������Ŀ�������С.
A. ���� B. ���� C. ���� D. ���϶�����
 C
��������������֪����ڴ���װ��5������3������2��������5+3+2=10������������ĸ����ǣ���������ĸ����ǣ���������ĸ����ǣ���ˣ���������Ŀ�������С.
��ѡC.
C
��������������֪����ڴ���װ��5������3������2��������5+3+2=10������������ĸ����ǣ���������ĸ����ǣ���������ĸ����ǣ���ˣ���������Ŀ�������С.
��ѡC. ���ڵ�O�����ĶԳƵ������ı���ABCD��DEFG��AD��BE��CF��DG����______
 ��O
����������Ӧ������߾����Գ�����.
�ʴ𰸣���O.
��O
����������Ӧ������߾����Գ�����.
�ʴ𰸣���O. 
