题目内容
16.先化简,再求值:(1-$\frac{3}{x+2}$)+$\frac{{x}^{2}-1}{x+2}$,其中x=$\sqrt{2}$-1.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{x-1}{x+2}$+$\frac{{x}^{2}-1}{x+2}$
=$\frac{{x}^{2}+x-2}{x+2}$
=$\frac{(x-1)(x+2)}{x+2}$
=x-1,
当x=$\sqrt{2}$-1时,原式=$\sqrt{2}$-1-1=$\sqrt{2}$-2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
6.下列命题是真命题的是( )
| A. | 有两条边和一个角分别对应相等的两个三角形全等 | |
| B. | 两边分别相等的两个直角三角形全等 | |
| C. | 一个锐角和一条边分别相等的两个直角三角形全等 | |
| D. | 斜边和一个锐角分别相等的两个直角三角形全等 |
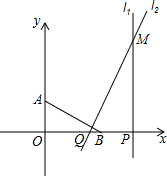 如图,点A(0,2)、B(4,0),点P从(8,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从B点出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<4)秒
如图,点A(0,2)、B(4,0),点P从(8,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从B点出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<4)秒