题目内容
7.已知:如图,线段AB=8,以A为圆心,5为半径作圆A,点C在⊙A上,过点C作CD∥AB交⊙A于点D(点D在C右侧),联结BC、AD.(1)若CD=6,求四边形ABC的面积;
(2)设CD=x,BC=y,求y与x的函数关系式及自变量x的取值范围;
(3)设BC的中点为M,AD的中点为N,线段MN交⊙A于点E,联结CE,当CD取何值时,CE∥AD.
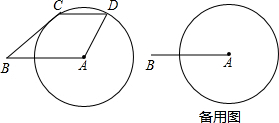
分析 (1)作AH⊥CD于H,如图,根据垂径定理得CH=DH=$\frac{1}{2}$CD=$\frac{1}{2}$×6=3,再利用勾股定理计算出AH=4,然后根据梯形的面积公式求解;
(2)作CP⊥AB于P,如图1,根据垂径定理得CH=DH=$\frac{1}{2}$x,易得AP=CH=$\frac{1}{2}$x,则BP=AB-AP=8-$\frac{1}{2}$x,在Rt△PAC中利用勾股定理得到CP2=25-$\frac{1}{4}$x2,在Rt△BPC中根据勾股定理得到y2=(8-$\frac{1}{2}$x)2+25-$\frac{1}{4}$x2=89-8x,然后利用算术平方根定义即可得到y与x的关系;
(3)设AH交MN于点F,连结AE,如图2,易得MN为梯形ABCD的中位线,则MN∥CD,当CE∥AD,则可判断四边形CEND为平行四边形,得到DC=NE=x,再证明FN为△AHD的中位线得到FN=$\frac{1}{2}$DH=$\frac{1}{4}$x,所以EF=$\frac{3}{4}$x,根据勾股定理得到AF2=AE2-EF2,AF2=AN2-NF2,则AE2-EF2=AN2-NF2,即52-($\frac{3}{4}$x)2=($\frac{5}{2}$)2-($\frac{1}{4}$x)2,然后解方程即可.
解答  解:(1)作AH⊥CD于H,如图,则CH=DH=$\frac{1}{2}$CD=$\frac{1}{2}$×6=3,
解:(1)作AH⊥CD于H,如图,则CH=DH=$\frac{1}{2}$CD=$\frac{1}{2}$×6=3,
在Rt△AHD中,∵AD=5,DH=3,
∴AH=$\sqrt{A{D}^{2}-D{H}^{2}}$=4,
∴四边形ABCD的面积=$\frac{1}{2}$(CD+AB)•AH=$\frac{1}{2}$×(6+8)×4=28;
(2)作CP⊥AB于P,如图1,
∵AH⊥CD,CD=x
∴CH=DH=$\frac{1}{2}$x,
∴AP=CH=$\frac{1}{2}$x,
∴BP=AB-AP=8-$\frac{1}{2}$x,
在Rt△PAC中,∵AC2=AP2+CP2,
∴CP2=25-$\frac{1}{4}$x2,
在Rt△BPC中,∵BC2=BP2+CP2,
∴y2=(8-$\frac{1}{2}$x)2+25-$\frac{1}{4}$x2=89-8x,
∴y=$\sqrt{89-8x}$(0<x<10); (3)设AH交MN于点F,连结AE,如图2,
(3)设AH交MN于点F,连结AE,如图2,
∵CD∥AB,CD≠AB,
∴四边形ABCD为梯形,
∵BC的中点为M,AD的中点为N,
∴MN为梯形ABCD的中位线,
∴MN∥CD,
∵CE∥AD,
∴四边形CEND为平行四边形,
∴DC=NE=x,
∵FN∥CD,N点为AD的中点,
∴FN为△AHD的中位线,
∴FN=$\frac{1}{2}$DH=$\frac{1}{4}$x,
∴EF=x-$\frac{1}{4}$x=$\frac{3}{4}$x,
在Rt△AEF中,AF2=AE2-EF2,
在Rt△AFN中,AF2=AN2-NF2,
∴AE2-EF2=AN2-NF2,即52-($\frac{3}{4}$x)2=($\frac{5}{2}$)2-($\frac{1}{4}$x)2,解得x=$\frac{5\sqrt{6}}{2}$.
即当CD为$\frac{5\sqrt{6}}{2}$时,CE∥AD.
点评 本题考查了圆的综合题:熟练掌握垂径定理、梯形的性质和平行四边形的判定与性质;会运用三角形中位线和梯形中位线性质得到有关线段的数量关系和位置关系;会运用勾股定理进行几何计算.

 步步高达标卷系列答案
步步高达标卷系列答案| A. | 掷一枚均匀的骰子,骰子停止转动后3点朝上是不可能事件 | |
| B. | 了解一批电视机的使用寿命,适合用抽样调查的方式 | |
| C. | 若a为实数,则|a|>0是必然事件 | |
| D. | 甲、乙两人各进行10次射击,两人射击成绩的方差分别为S${\;}_{甲}^{2}$=2,S${\;}_{乙}^{2}$=4,则乙的射击成绩更稳定 |
 某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:
某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:频数分布表
| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 25≤x<30 | 4 |
| 第2组 | 30≤x<35 | 8 |
| 第3组 | 35≤x<40 | 16 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 10 |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请你估计该校八年级汉字书写优秀的人数?
(4)第一组中的A、B、C、D 四名同学为提高汉字书写能力,分成两组,每组两人进行对抗练习,请用列表法或画树状图的方法,求A与B名同学能分在同一组的概率.
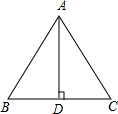 如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )
如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )| A. | ∠B=45° | B. | ∠BAC=90° | C. | BD=AC | D. | AB=AC |
| 质量/kg | 0.5 | 0.6 | 0.7 | 1.0 | 1.2 | 1.6 | 1.9 |
| 数量/条 | 1 | 8 | 15 | 18 | 5 | 1 | 2 |
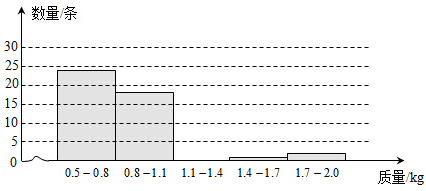
(1)请根据表中数据补全下面的直方图(各组中数据包括左端点不包括右端点).
(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1kg).