题目内容
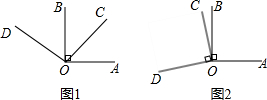
11.如图1,已知AO⊥OB,∠BOD=∠AOC.(1)试猜想OC与OD的位置关系,并说明理由;
(2)试猜想∠AOD与∠BOC的数量关系,并说明理由;
(3)若OA与OB,OC与OD的位置关系不变,当∠COD绕点O不停地转动,如旋转到图2的位置,(2)中的结论还成立吗?并说明理由.
分析 (1)由垂直的定义可知:∠AOC+∠BOC=90°,然后根据∠BOD=∠AOC,可得到∠DOC=90°;
(2)由∠AOC+∠BOC=90°,∠BOC+∠BOD=90°证明即可;
(3)依据周角是360°进行证明即可.
解答 解:(1)OC⊥OD.
理由:∵AO⊥OB,
∴∠AOC+∠BOC=90°.
∵∠BOD=∠AOC,
∴∠BOC+∠BOD=90°.
∴OC⊥OD.
(2)∠AOD+∠BOC=180°.
理由:∵∠AOC+∠BOC=90°,∠BOC+∠BOD=90°,
∴∠AOC+∠BOC+∠BOC+∠BOD=180°.
∵∠AOC+∠BOC+∠BOD=∠AOD,
∴∠AOD+∠BOC=180°.
(3)成立.
理由:∵∠AOD+∠BOC+∠COD+∠AOB=360°,
∴∠AOD+∠BOC+180°=360°.
∴∠AOD+∠BOC=180°.
点评 本题主要考查的是补角和余角的定义,掌握图形中角的和差关系是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
2.已知R=$\frac{2008×2009}{2010×2011}$,S=$\frac{2008×2010}{2009×2011}$,T=$\frac{2008×2011}{2009×2010}$,则( )
| A. | R>S>T | B. | T>S>R | C. | S>T>R | D. | S>R>T |
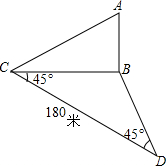 为了求河对岸建筑物AB的高,在地平面上测得基线CD=180米,在C点测得A点的仰角为30°,在地平面上测得∠BCD=∠BDC=45°,那么AB的高是30$\sqrt{6}$米.
为了求河对岸建筑物AB的高,在地平面上测得基线CD=180米,在C点测得A点的仰角为30°,在地平面上测得∠BCD=∠BDC=45°,那么AB的高是30$\sqrt{6}$米.