题目内容

1．因式分解：
（1）4（3x+y）2-（2x-y）2；
（2）x5y3-x3y5；
（3）（x+y+z）2-（x-y-z）2
（4）81x4-16y4．

分析 （1）原式利用平方差公式分解即可；
（2）原式提取公因式，再利用平方差公式分解即可；
（3）原式利用平方差公式分解即可；
（4）原式利用平方差公式分解即可．

解答 解：（1）原式=[2（3x+y）+（2x-y）][2（3x+y）-（2x-y）]=（8x+y）（4x+3y）；
（2）原式=x3y3（x2-y2）=x3y3（x+y）（x-y）；
（3）原式=（x+y+z+x-y-z）（x+y+z-x+y+z）=4x（y+z）；
（4）原式=（9x2+4y2）（9x2-4y2）=（9x2+4y2）（3x+2y）（3x-2y）．

点评 此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．

练习册系列答案
相关题目
11．如图1，已知AO⊥OB，∠BOD=∠AOC．
（1）试猜想OC与OD的位置关系，并说明理由；
（2）试猜想∠AOD与∠BOC的数量关系，并说明理由；
（3）若OA与OB，OC与OD的位置关系不变，当∠COD绕点O不停地转动，如旋转到图2的位置，（2）中的结论还成立吗？并说明理由．
12．一圆柱形容器盛有$\frac{4}{5}$容积的酒精，从中倒出20L后，容器中的酒精还占这个容器容积的$\frac{2}{3}$，这个容器的容积是150L．
9．计算：
（1）$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$÷$\frac{x-1}{{x}^{2}+x}$
（2）$\frac{{x}^{2}-4{y}^{2}}{{x}^{2}+2xy+{y}^{2}}÷\frac{x+2y}{{x}^{2}+xy}$．
16．小明a分钟打了b个字，小亮m分钟打了n个字，则小明每分钟打字$\frac{b}{a}$个，小亮每分钟打字$\frac{n}{m}$个，小明每分钟打字的速度是小亮每分钟打字速度的$\frac{bm}{an}$倍．
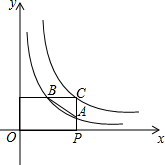6．如图，已知反比例函数y=$\frac{a}{x}$和y=$\frac{b}{x}$（a≠0，b≠0），P（c，0）是x轴上的一个动点，过点P作x轴的垂线分别交y=$\frac{a}{x}$和y=$\frac{b}{x}$的图象于点A，C，过点C作y轴的垂线交y=$\frac{a}{x}$的图象于点B，连接AB，设△ABC的面积为S．
（1）当a=1，b=4，c=3时，求S的值；
（2）若a=1，b=4，c＞0，根据这些条件能否求出S的值？请说明理由．
13．问题情境：先化简，再求值：（x-1-$\frac{3}{x+1}$）÷$\frac{{x}^{2}+4x+4}{x+1}$，其中x=7．
解法展示：原式=（$\frac{x-1}{1}$-$\frac{3}{x+1}$）÷$\frac{{x}^{2}+4x+4}{x+1}$=（$\frac{{x}^{2}-1}{x+1}$-$\frac{3}{x+1}$）÷$\frac{{x}^{2}+4x+4}{x+1}$（根据1）=$\frac{{x}^{2}-1-3}{x+1}$÷$\frac{{x}^{2}+4x+4}{x+1}$=$\frac{（x+2）（x-2）}{x+1}$•$\frac{x+1}{（x+2）^{2}}$（根据2）=$\frac{x-2}{x+2}$．
当x=7时，原式=$\frac{7-2}{7+2}$=$\frac{5}{9}$．
反思交流：
（1）上述解法中的根据1是指分式的分子分母同时乘以同一个不为0的整式，分式的值不变，根据2是指分式的分子分母同时除以同一个不为0的整式，分式的值不变．
（2）上述解法的运算顺序是先计算括号中的减法运算，再计算除法运算．
（3）利用上述解法解答下列问题：先化简，再求值：$\frac{{x}^{2}+2x+1}{2x-6}$÷（x-$\frac{1-3x}{x-3}$），其中x=5．
10．如图，在△ABC中，AD⊥BC于点D，过点D作DE∥AC，DF∥AB，分别交AB，AC于点E，F，当△ABC满足什么条件时，四边形AEDF是菱形．
11．解下列分式方程：
（1）$\frac{2}{x+1}$+$\frac{3}{x-1}$=$\frac{6}{{x}^{2}-1}$；（2）$\frac{x}{x-2}$+$\frac{6}{x+2}$=1；
（3）$\frac{3}{x-2}$+$\frac{x-3}{2-x}$=1；（4）$\frac{x+3}{{x}^{2}+x}$+2=$\frac{2x}{x+1}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网