题目内容
1.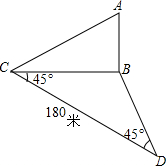 为了求河对岸建筑物AB的高,在地平面上测得基线CD=180米,在C点测得A点的仰角为30°,在地平面上测得∠BCD=∠BDC=45°,那么AB的高是30$\sqrt{6}$米.
为了求河对岸建筑物AB的高,在地平面上测得基线CD=180米,在C点测得A点的仰角为30°,在地平面上测得∠BCD=∠BDC=45°,那么AB的高是30$\sqrt{6}$米.
分析 根据∠BCD=∠BDC=45°,于是得到∠CBD=90°,CB=BD,根据等腰直角三角形的性质得到CB=DB=90$\sqrt{2}$,解直角三角形即可得到结论.
解答 解:∵∠BCD=∠BDC=45°,
∴∠CBD=90°,CB=BD,
∵CD=180米,
∴CB=DB=90$\sqrt{2}$,
∵∠ACB=30°,∠ABC=90°,
∴AB=BC•tan30°=30$\sqrt{6}$米.
故答案为:30$\sqrt{6}$.
点评 本题考查了解直角三角形的应用-仰角和俯角,熟练掌握三角函数的定义是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,在梯形ABCD中,EF与AD、BC平行,GH、IJ均与AB平行,GM、KL均与DC平行,图中共有22个梯形.
如图,在梯形ABCD中,EF与AD、BC平行,GH、IJ均与AB平行,GM、KL均与DC平行,图中共有22个梯形.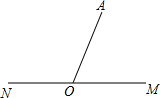 如图所示,O是直线MN上的任意一点,射线OA为过O点的一条射线,且∠N0A=115°.
如图所示,O是直线MN上的任意一点,射线OA为过O点的一条射线,且∠N0A=115°.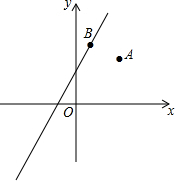 如图:点A的坐标为(3,4),点B在直线y=2x+4上运动,当线段AB最短时,AB的长度为$\frac{6}{5}$$\sqrt{5}$.
如图:点A的坐标为(3,4),点B在直线y=2x+4上运动,当线段AB最短时,AB的长度为$\frac{6}{5}$$\sqrt{5}$.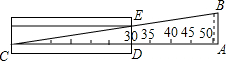 如图,刻度尺的分度值为1mm,如果玻璃管的内径DE正对“30”刻度线(DE∥AB).且量得AB长7mm,那么DE的长应为多少?如果DE正对“35”刻度线呢?
如图,刻度尺的分度值为1mm,如果玻璃管的内径DE正对“30”刻度线(DE∥AB).且量得AB长7mm,那么DE的长应为多少?如果DE正对“35”刻度线呢?