题目内容
15．
如图所示，AB为⊙O的直径，AB=6，∠CAD=30°，则弦DC=3．
分析 连接OC，OD，证明△OCD是等边三角形，得出DC=OC即可．
解答 解：连接OC、OD，如图，
∵∠CAD=30°，
∴∠COD=2∠CAD=60°，
∵OC=OD，
∴△OCD是等边三角形，
∴DC=OC=$\frac{1}{2}$AB=3；
故答案为：3．
点评 本题考查了圆周角定理、等边三角形的判定；熟练掌握圆周角定理，证明三角形是等边三角形是解决问题的关键．
练习册系列答案
相关题目
13．下列说法中正确的是（ ）
| A． | 平分弦的直径垂直于弦 | |
| B． | 圆心角是圆周角的2倍 | |
| C． | 三角形的外心到三角形各边的距离相等 | |
| D． | 从圆外一点可以引圆的两条切线，这一点和圆心的连线平分两条切线的夹角 |
如图，已知DC是∠ACB的外角平分线，∠BAC与∠1的大小关系如何？∠BAC与∠2呢？∠2与∠B呢？∠BAC与∠B呢？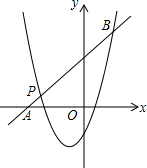
已知二次函数y1=x2+mx+n的图象经过点P（-3，1），对称轴是经过（-1，0）且平行于y轴的直线．
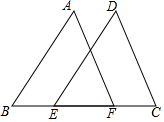如图，已知点E、F在BC上，且BE=CF，AB=CD，∠B=∠C，试说明△ABF≌△DCE．
20．已知Rt△ABC中，∠C=90°，AC=1，BC=3，则AB的取值范围是（ ）
| A． | 3.0＜AB＜3.1 | B． | 3.1＜AB＜3.2 | C． | 3.2＜AB＜3.3 | D． | 3.3＜AB＜3.4 |
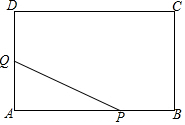如图，在矩形ABCD中，AB=12cm，BC=9cm．P、Q两点同时从点B、D出发，分别沿BA、DA方向匀速运动（当P运动到A时，P、Q同时停止运动），已知P点的速度比Q点大1cm/s，设P点的运动时间为x秒，△PAQ的面积为ycm2，
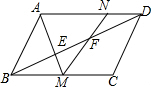如图，平行四边形ABCD周长为40，∠ABC=60°，E，F在BD上，BE=EF=FD，AE的延长线交BC于M，MF的延长线交AD于N，设BC=x，△ANM的面积为y，求y关于x的函数解析式．