题目内容
17.某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克,针对这种海产品的销售情况,请解答以下问题:(1)当销售单价定为每千克55元时,月销售量是450千克,月销售利润是6750元;
(2)设销售单价为每千克x元,月销售利润为y,请你求出y与x之间的函数关系式;
(3)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应该定为多少元?
分析 (1)根据月销售量为=500-(销售单价-50)×10,即可得出结论,再根据月销售利润=销售每千克的利润×销售数量,代入数据即可得出结论;
(2)根据月销售利润=销售每千克的利润×销售数量,即可得出y与x之间的函数关系式;
(3)令y=-10x2+1400x-40000=8000,解一元二次方程即可得出x的值,再根据月销售成本不超过10000元即可得出关于x的一元一次不等式,解之即可得出x的取值范围,由此即可确定x的值.
解答 解:(1)当销售单价定为每千克55元时,月销售量为500-(55-50)×10=450(千克),
月销售利润为(55-40)×450=6750(元).
故答案为:450;6750.
(2)根据题意得:y=(x-40)[500-(x-50)×10]=-10x2+1400x-40000.
(3)当y=8000时,有-10x2+1400x-40000=8000,
解得:x1=80,x2=60.
∵x[500-(x-50)×10]=400(100-x)≤10000,
解得:x≥75,
∴x=80.
答:销售单价定为80元.
点评 本题考查了一元二次方程的应用以及解一元一次不等式,根据数量关系列出一元二次方程(或列式计算)是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
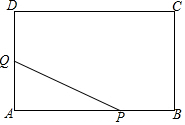 如图,在矩形ABCD中,AB=12cm,BC=9cm.P、Q两点同时从点B、D出发,分别沿BA、DA方向匀速运动(当P运动到A时,P、Q同时停止运动),已知P点的速度比Q点大1cm/s,设P点的运动时间为x秒,△PAQ的面积为ycm2,
如图,在矩形ABCD中,AB=12cm,BC=9cm.P、Q两点同时从点B、D出发,分别沿BA、DA方向匀速运动(当P运动到A时,P、Q同时停止运动),已知P点的速度比Q点大1cm/s,设P点的运动时间为x秒,△PAQ的面积为ycm2,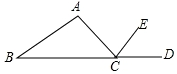 如图,AB=AC,∠A=100°,CE平分∠ACD,求∠ECD的度数.
如图,AB=AC,∠A=100°,CE平分∠ACD,求∠ECD的度数.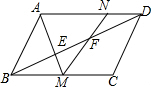 如图,平行四边形ABCD周长为40,∠ABC=60°,E,F在BD上,BE=EF=FD,AE的延长线交BC于M,MF的延长线交AD于N,设BC=x,△ANM的面积为y,求y关于x的函数解析式.
如图,平行四边形ABCD周长为40,∠ABC=60°,E,F在BD上,BE=EF=FD,AE的延长线交BC于M,MF的延长线交AD于N,设BC=x,△ANM的面积为y,求y关于x的函数解析式.