题目内容
12.若关于x、y的多项式xm-1y-nxm-2y+2xm-3y+4xm-2y-3xm-3y2+2xm-1y为五次三项式,那么(-1)m$\frac{n}{m}$+(-1)n$\frac{m}{n}$=$\frac{9}{20}$.分析 首先合并同类项,再根据多项式的意义确定哪一项为0,求得m、n的数值,代入求得答案即可.
解答 解:∵原式=3xm-1y+(4-n)xm-2y+2xm-3y-3xm-3y2为五次三项式,
∴4-n=0,m-1=4,
解得:m=5,n=4,
∴(-1)m$\frac{n}{m}$+(-1)n$\frac{m}{n}$=-$\frac{4}{5}$+$\frac{5}{4}$=$\frac{9}{20}$.
故答案为:$\frac{9}{20}$.
点评 本题考查了与多项式有关的概念,解题的关键理解五次三项式的概念,多项式中每个单项式叫做多项式的项,有几项叫几项式,这些单项式中的最高次数,就是这个多项式的次数.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
3.若a>b,则下列式子一定成立的是( )
| A. | a+3>b+5 | B. | 1-a>1-b | C. | a-9>b-9 | D. | ac2>bc2 |
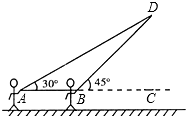 放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,最后结果精确到1米).
放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,最后结果精确到1米).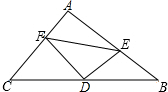 如图所示,在△ABC中,∠A=90°,D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试探究线段BE,EF,FC之间的数量关系.
如图所示,在△ABC中,∠A=90°,D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试探究线段BE,EF,FC之间的数量关系. 如图,△ABC与△DBE都是等边三角形.
如图,△ABC与△DBE都是等边三角形.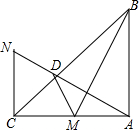 如图,AB⊥AC,NC⊥AC,AB=AC,M为AC中点,AN⊥BM交BC于D,BC平分∠ACN.求证:
如图,AB⊥AC,NC⊥AC,AB=AC,M为AC中点,AN⊥BM交BC于D,BC平分∠ACN.求证: