题目内容
2.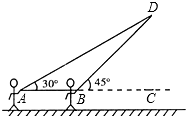 放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,最后结果精确到1米).
放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,最后结果精确到1米).
分析 作DH⊥BC于H,设DH=x米,根据三角函数表示出AH于BH的长,根据AH-BH=AB得到一个关于x的方程,解方程求得x的值,进而求得AD-BD的长,即可解题.
解答  解:作DH⊥BC于H,设DH=x米.
解:作DH⊥BC于H,设DH=x米.
∵∠ACD=90°,
∴在直角△ADH中,∠DAH=30°,AD=2DH=2x,AH=DH÷tan30°=$\sqrt{3}$x,
在直角△BDH中,∠DBH=45°,BH=DH=x,BD=$\sqrt{2}$x,
∵AH-BH=AB=10米,
∴$\sqrt{3}$x-x=10,
∴x=5($\sqrt{3}$+1),
∴小明此时所收回的风筝的长度为:
AD-BD=2x-$\sqrt{2}$x=(2-$\sqrt{2}$)×5($\sqrt{3}$+1)≈(2-1.414)×5×(1.732+1)≈8米.
答:小明此时所收回的风筝线的长度约是8米.
点评 本题考查了直角三角形的运用,考查了30°角所对直角边是斜边一半的性质,本题中求得DH的长是解题的关键.

练习册系列答案
相关题目

 如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )
如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( ) 如图,AB是⊙0的直径,PQ是⊙0的切线,切点为C,求证:∠PCA=∠B.
如图,AB是⊙0的直径,PQ是⊙0的切线,切点为C,求证:∠PCA=∠B. 如图,O2是⊙O1上的一点,以O2为圆心,O1O2为半径作⊙O2,与⊙O1交于点A、B,那么∠AO1B的度数为120°.
如图,O2是⊙O1上的一点,以O2为圆心,O1O2为半径作⊙O2,与⊙O1交于点A、B,那么∠AO1B的度数为120°.