题目内容
在矩形ABCD中对角线AC,BD相交于点O,∠AOB=60°,AC=10cm,则AB的长为( )
| A、3cm | B、4cm |
| C、5cm | D、10cm |
考点:矩形的性质
专题:
分析:利用矩形的性质得出AO=CO=BO=DO=5cm,再利用等边三角形的判定得出即可.
解答: 解:如图所示:∵在矩形ABCD中对角线AC,BD相交于点O,∠AOB=60°,AC=10cm,
解:如图所示:∵在矩形ABCD中对角线AC,BD相交于点O,∠AOB=60°,AC=10cm,
∴AO=CO=BO=DO=5cm,则△ABO是等边三角形,
∴AB的长为5cm.
故选:C.
 解:如图所示:∵在矩形ABCD中对角线AC,BD相交于点O,∠AOB=60°,AC=10cm,
解:如图所示:∵在矩形ABCD中对角线AC,BD相交于点O,∠AOB=60°,AC=10cm,∴AO=CO=BO=DO=5cm,则△ABO是等边三角形,
∴AB的长为5cm.
故选:C.
点评:此题主要考查了矩形的性质以及等边三角形的判定,得出△ABO是等边三角形是解题关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知抛物线y=ax2+bx+c(a<0)的对称轴为x=1,交x轴的一个交点为(x1,0),且-1<x1<0,有下列5个结论:①abc>0;②9a-3b+c<0;③2c<3b;④(a+c)2<b2;⑤a+b>m(am+b)(m≠1的实数)其中正确的结论有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知Rt△ABC中,∠C=90°,BC=8,AB=10,则sinA=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
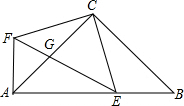 如图,在等腰Rt△ABC中,AC=BC,∠ACB=90°,点E在线段AB上,CF⊥CE,CF=CE,EF交AC于G,连接AF.
如图,在等腰Rt△ABC中,AC=BC,∠ACB=90°,点E在线段AB上,CF⊥CE,CF=CE,EF交AC于G,连接AF.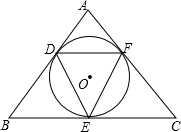 如图,⊙O是△ABC的内切圆,D、E、F是切点,D、E、F分别在AB、BC、CA上.问:△DEF的形状有什么特点?
如图,⊙O是△ABC的内切圆,D、E、F是切点,D、E、F分别在AB、BC、CA上.问:△DEF的形状有什么特点? 如图所示,已知△ABC中,DE∥BC,AD=2,BD=5,AC=5,求AE的长.
如图所示,已知△ABC中,DE∥BC,AD=2,BD=5,AC=5,求AE的长. 画出△ABC关于原点对称的图形△DEF,并写出D、E、F的坐标.
画出△ABC关于原点对称的图形△DEF,并写出D、E、F的坐标.