题目内容
如图所示，D，E分别是△ABC的边AC．BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数为 （ ）
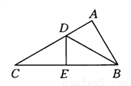
A. 15° B. 20° C. 25° D. 30°
D
【解析】∵△ADB≌△EDB≌△EDC，
∴∠C=∠DBE=∠DBA，∠DEC=∠DEB=∠A=90°，
∴∠C=30°
故选D.
练习册系列答案
相关题目
如图,下列推理正确的有( )
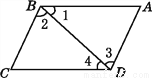
①因为∠1=∠4,所以BC∥AD;
②因为∠2=∠3,所以AB∥CD;
③因为∠BCD+∠ADC=180°,所以AD∥BC;
④因为∠1+∠2+∠C=180°,所以BC∥AD.
A. 1个 B. 2个 C. 3个 D. 4个
A
【解析】（1）由∠1=∠2不能推导出BC∥AD，所以①中的推理错误；
（2）由∠2=∠3不能推导出AB∥CD，所以②中的推理错误；
（3）由∠BCD+∠ADC=180°能推导出BC∥AD，所以③中推理正确；
（4）由∠BCD+∠ABC=180°不能推导出BC∥AD，所以④中推理错误；
即4个推理中，只有③正确.
故选A. 如图,已知零件的外径为a,要求它的厚度x,动手制作一个简单的工具,利用三角形全等的知识,求出x.
.
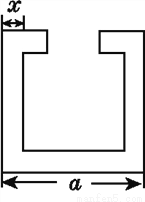
【解析】试题分析：可设计如图所示的工具,利用△AOB≌△COD即可求解.
试题解析：可设计如图所示的工具,其中O为AC,BD的中点.
在△AOB和△COD中,
所以△AOB≌△COD(SAS).
所以AB=CD.所以测量出C,D之间的距离,CD的长就是A,B间的距离.
因为AB=a-2x,所以x==. 如图，AB=CD，AD=CB，那么下列结论中错误的是（ ）
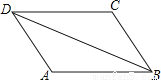
A. ∠A=∠C B. AB=AD C. AD∥BC D. AB∥CD
B
【解析】∵在△ABD和△CDB中，
，
∴△ABD≌△CDB，
∴∠ADB=∠CBD，∠ABD=∠CDB，∠A=∠C
∴AD∥BC，AB∥CD，
∴A、C、D选项正确.
故选：B. 如图,△ACB与△BDA全等,AC与BD对应,BC与AD对应,写出其余的对应边和对应角.
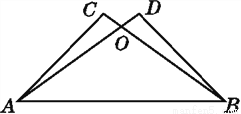
见解析
【解析】试题分析：利用全等三角形的性质分别得出对应点进而得出对应边与对应角关系．
试题解析: ∵ △ACB≌△BDA,
∴AB=BA;∠CBA=∠DAB,∠CAB=∠DBA,∠C=∠D. 如图,沿直线AC对折,△ABC与△ADC重合,则△ABC≌___________,AB的对应边是___________,∠BCA的对应角是___________.
△ADC AD ∠DCA
【解析】本题考查的是全等三角形的性质
根据全等三角形的对应边相等、对应角相等即可判断， （10分）在△ABC中，BE、CF分别是AC、AB两条边上的高，在BE上截取BD＝AC，在CF的延长线上截取CG＝AB，连结AD、AG。求证：AG＝AD
可证明△EBM≌△FCM，
得∠EMB≌△FCM，
得∠EMB＝∠FMC，
∵∠CMF＋∠BMF＝180°
∴∠BME＋∠BMF＝180°
∴E、F、M恰好在一直线上
【解析】分析：三角形全等条件中必须是三个元素，本题已经有两条对应边相等，只要再找到它们的夹角相等就可以了．
解答：证明：∵BE、CF分别是AC、AB两条边上的高，
∴∠ABD+∠BAC... 已知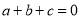
， 
.
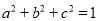（1）求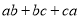
的值；
（2）求
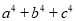的值．
（1） （2）
【解析】试题分析：（1）把a+b+c=0两边平方，然后利用代入法等量代换即可；
（2）把ab+bc+ca与两边分别乘方即可.
试题解析：（1）因为a+b+c=0
所以+2ab+2ac+2bc=0
∴2ab+2ac+2bc=-1
即ab+bc+ca=-
（2）因为a+b+c=0，a2+b2+c2=1
所以+2ab+2ac+2bc=0
... 如果(2x＋m)(x－5)展开后的结果中不含x的一次项，那么m等于( )
A. 5 B. －10 C. －5 D. 10
D
【解析】(2x＋m)(x－5)=2x2+mx-10x-5m，因展开后的结果中不含x的一次项，可得m-10=0，解得m=10，故选D.