题目内容
6.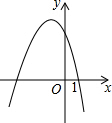 二次函数y=ax2+bx+c的图象如图所示,则化简二次根式$\sqrt{(a+c)^{2}}$+$\sqrt{(b-c)^{2}}$的结果是( )
二次函数y=ax2+bx+c的图象如图所示,则化简二次根式$\sqrt{(a+c)^{2}}$+$\sqrt{(b-c)^{2}}$的结果是( )| A. | a+b | B. | -a-b | C. | 2b-c | D. | -2b+c |
分析 根据二次函数的图象确定a,b,c的取值范围后再化简二次根式.
解答 解:由图知,二次函数y=ax2+bx+c的图象的开口向,a<0,
与y轴交于y轴的正半轴,c>0,
对称轴在二象限,-$\frac{b}{2a}$<0,a<0,则b<0,
图象过点(1,0),
因此a+b+c=0,a+c=-b>0,
所以原式=a+c+c-b=-b+c-b=-2b+c.
故选D.
点评 本题利用了二次函数的图象确定a,b,c的取值范围后再化简二次根式,注意二次根式的结果为非负数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
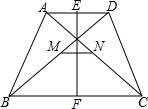 已知:如图,在梯形ABCD中,AD∥DC,AB=DC,E,F,M,N分别是AD,BC,BD,AC的中点.猜想EF与MN的关系,并证明.
已知:如图,在梯形ABCD中,AD∥DC,AB=DC,E,F,M,N分别是AD,BC,BD,AC的中点.猜想EF与MN的关系,并证明.
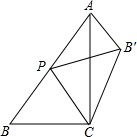 如图,在△ABC中,∠ACB=90°,AB=10,AC=8,P是AB边上的动点(不与点B重合),点B关于直线CP的对称点是B′,连接B′A,则B′A长度的最小值是2.
如图,在△ABC中,∠ACB=90°,AB=10,AC=8,P是AB边上的动点(不与点B重合),点B关于直线CP的对称点是B′,连接B′A,则B′A长度的最小值是2.
 如图,在△ABC中,AB=AC,AD⊥BC,E是AC的中点.若DE=5,则AB的长为10,若AD=8,则BC=12.
如图,在△ABC中,AB=AC,AD⊥BC,E是AC的中点.若DE=5,则AB的长为10,若AD=8,则BC=12.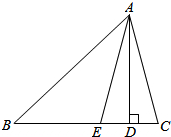 如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.
如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.