题目内容
11.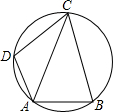 如图,在圆的内接四边形ABCD中,对角线AC平分∠DAB,若∠DAB=120°,AD=1,AC=3.4,求线段AB的长.
如图,在圆的内接四边形ABCD中,对角线AC平分∠DAB,若∠DAB=120°,AD=1,AC=3.4,求线段AB的长.
分析 先求出$\widehat{CD}=\widehat{BC}$,得出CD=BC,由余弦定理得出BC2=AB2+AC2-2AB•AC•cos∠BAC=9.16,设AB=x,得出方程:x2-3.4x+2.4=0,解方程即可.
解答 解:∵AC平分∠DAB,∠DAB=120°,
∴∠DAC=∠BAC=60°,
∴$\widehat{CD}=\widehat{BC}$,
∴CD=BC,
由余弦定理得:CD2=AD2+AC2-2AD•AC•cos∠DAC=12+3.42-2×1×3.4×$\frac{1}{2}$=9.16,
∴BC2=AB2+AC2-2AB•AC•cos∠BAC=9.16,
设AB=x,则x2+3.42-2x×3.4×$\frac{1}{2}$=9,16,
即 x2-3.4x+2.4=0,
解得:x=1,或x=2.4,
∴AB的长为:1或2.4.
点评 本题考查了圆周角定理、余弦定理;熟练掌握圆周角定理,运用余弦定理得出方程是解决问题的关键.

练习册系列答案
相关题目
2. 如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )
如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )
 如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )
如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )| A. | 折扇大 | B. | 团扇大 | C. | 一样大 | D. | 不能比较 |
19.方程$2{x^2}-3x=\frac{1}{2}({{x^2}-6x})$的解是( )
| A. | 0,0 | B. | 0,3 | C. | 0,2 | D. | 0,$\frac{1}{3}$ |
16.下列各点中在抛物线y=x2-4x-4上的点是( )
| A. | (4,4) | B. | (3,-1) | C. | (-2,-8) | D. | (-$\frac{1}{2}$,-$\frac{7}{4}$) |
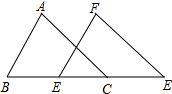 如图,B、C、D、E在同一直线上,已知AB∥FC,AB=FC,BC=DE,求证:AD${\;}_{=}^{∥}$FE.
如图,B、C、D、E在同一直线上,已知AB∥FC,AB=FC,BC=DE,求证:AD${\;}_{=}^{∥}$FE. 如图,已知BC是⊙O的直径,AB是⊙O的弦,OD⊥AB于点P,交劣弧AB于点D.
如图,已知BC是⊙O的直径,AB是⊙O的弦,OD⊥AB于点P,交劣弧AB于点D. 已知,∠ABC=∠DBE=90°,且AB=BC,BE=BD,说明:S△ABE=S△BCD.
已知,∠ABC=∠DBE=90°,且AB=BC,BE=BD,说明:S△ABE=S△BCD.