题目内容
1. 已知,∠ABC=∠DBE=90°,且AB=BC,BE=BD,说明:S△ABE=S△BCD.
已知,∠ABC=∠DBE=90°,且AB=BC,BE=BD,说明:S△ABE=S△BCD.
分析 作EG⊥AB,交AB的延长线与点G,作DF⊥BC,垂足为F,可证△BEG≌△BDF,得EG=DF,然后用三角形面积格式表示得证.
解答 证明:如图所示,作EG⊥AB,交AB的延长线与点G,作DF⊥BC,垂足为F,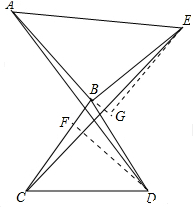
则∠G=∠BFD=∠CBG=∠DBE=90°,
∴∠DBF=90°-∠DBG=∠EBG,
在△BEG和△BDF中,
$\left\{\begin{array}{l}{∠G=∠BFD}\\{∠DBF=∠EBG}\\{BD=BE}\end{array}\right.$,
∴△BEG≌△BDF(AAS),
∴EG=DF
∵AB=BC
∴S△ABE=$\frac{1}{2}AB•EG=\frac{1}{2}BC•DF$=S△BCD.
点评 本题考查了三角形全的判定与性质以及等底等高的三角形面积相等,通过辅助线作出高有一定难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列说法:①已知a=8-b,c2=ab-16,则a=b;②已知a=22015,b=(-2)2015,则4a2-8ab+4b2=22034;③已知a+b=3,ab=-1,则a4+b4=45.其中正确的是( )
| A. | ①②③ | B. | ①② | C. | ① | D. | ② |
11. 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | $\sqrt{3}$+2 |
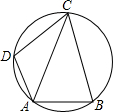 如图,在圆的内接四边形ABCD中,对角线AC平分∠DAB,若∠DAB=120°,AD=1,AC=3.4,求线段AB的长.
如图,在圆的内接四边形ABCD中,对角线AC平分∠DAB,若∠DAB=120°,AD=1,AC=3.4,求线段AB的长.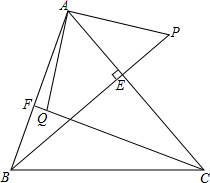 如图,已知BE是△ABC的高,点F是AB上一点,点P为BE延长线上的一点,点Q为CF上的一点,△PAB≌△AQC,则AP与AQ有怎样的关系?请说明理由.
如图,已知BE是△ABC的高,点F是AB上一点,点P为BE延长线上的一点,点Q为CF上的一点,△PAB≌△AQC,则AP与AQ有怎样的关系?请说明理由. 如图,在△ABC中,AC=BC,∠ACB=90°,延长BC到D,使BD=BA,BE⊥AD于点E,交AC于点F.
如图,在△ABC中,AC=BC,∠ACB=90°,延长BC到D,使BD=BA,BE⊥AD于点E,交AC于点F.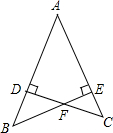 已知CD⊥AB,BE⊥AC,AB=AC,求证:DF=EF.
已知CD⊥AB,BE⊥AC,AB=AC,求证:DF=EF.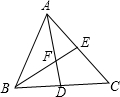 如图,△ABC的中线AD、BE相交于点F,若△ABF的面积为1,则四边形FDCE的面积是1.
如图,△ABC的中线AD、BE相交于点F,若△ABF的面积为1,则四边形FDCE的面积是1.