题目内容
7.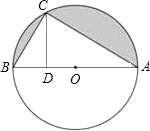 如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,且AB=8,DB=2.
如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,且AB=8,DB=2.(1)求证:△ABC∽△ACD;
(2)求图中阴影部分的面积.
分析 (1)根据两角对应相等的两个三角形相似即可证明.
(2)先利用△ABC∽△ACD,得AC2=AD•AB=48,再利用勾股定理求出CD,根据S阴=S半圆-S△ABC即可解决问题.
解答 (1)证明: ∵AB是直径,
∵AB是直径,
∴∠ACB=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ADC=∠ACB,∠B+∠BAC=90°,∠DCA+∠CAB=90°,
∴∠B=∠ACD,
∴△ABC∽△ACD.
(2)解:∵△ABC∽△ACD,
∴$\frac{AB}{AC}$=$\frac{AC}{AD}$,
∴AC2=AD•AB=6×8=48,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{48-36}$=2$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$•AB•CD=$\frac{1}{2}$×$8×2\sqrt{3}$=8$\sqrt{3}$,
∴S阴=S半圆-S△ABC=8$π-8\sqrt{3}$.
点评 本题考查相似三角形的判定和性质、圆的有关知识、勾股定理等知识,解题的关键是熟练掌握相似三角形的判定和性质,属于基础题,中考常考题型.

练习册系列答案
相关题目
17.已知下列命题
①若|a|=|b|,则a2=b2
②若a>0,b>0,则a+b>0
③到线段两端点距离相等的点在这条线段的垂直平分线上
④矩形的对角线相等
其中原命题与逆命题均为真命题的个数是( )
①若|a|=|b|,则a2=b2
②若a>0,b>0,则a+b>0
③到线段两端点距离相等的点在这条线段的垂直平分线上
④矩形的对角线相等
其中原命题与逆命题均为真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.一组数据2、9、5、5、8、5、8的中位数是( )
| A. | 2 | B. | 5 | C. | 8 | D. | 9 |
 如图,在8×5的正方形网格中,每个小正方形的边长都为1,点A在格点(网格线的交点)上,且点A的坐标为(0,4).
如图,在8×5的正方形网格中,每个小正方形的边长都为1,点A在格点(网格线的交点)上,且点A的坐标为(0,4).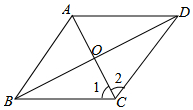 如图,菱形ABCD对角线AC,BD相交于点O,有下列结论:
如图,菱形ABCD对角线AC,BD相交于点O,有下列结论: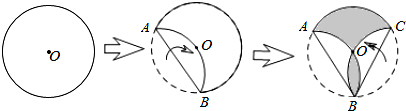
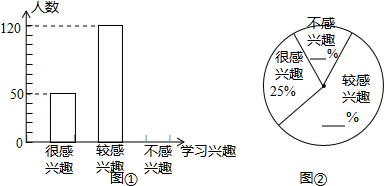
 如图,在边长为2的正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.
如图,在边长为2的正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP. 将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,若这个三角形面积的最小值为4.5cm2时,则纸片的宽为3.
将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,若这个三角形面积的最小值为4.5cm2时,则纸片的宽为3.